Out of this World…
story by Helen Hill
Internal convection on a gas giant using MITjcm - High Taylor number simulations are dominated by Taylor columns parallel to the axis of rotation (image source - Yohai Kaspi)
This month we look at work by Yohai Kaspi (a NOAA Climate and Global Change postdoctoral fellow currently working with Tapio Schneider at Caltech) who has been using MITgcm to model the atmosphere on a Jupiter-like gas giant.
The circulations on the gas giants are quite different from those in Earth’s atmosphere: The flows are dominantly zonal with only occasional vortices or waves rather than large populations of strong synoptic eddies within meridional flows as large as the zonal ones. The gas giants also have significant internal heat sources and sinks (gravitational collapse and core cooling) besides sharing an external (solar) heat source. While the pioneer and Voyager spacecrafts and the more recent Galileo and Cassini missions have yielded tremendous data bases, many questions such as the energy source, the depth, the stability and the structure of the jets remains unresolved. Taking a conventional release of MITgcm as their starting point, Kaspi and co-workers have developed a new general circulation model to try to understand more fully the role of rotation, a large vertical density gradient, internal heat sources, and their interaction with external solar heating in the context of a Jupiter-like planetary atmosphere.
The Model
Working with Glenn Flierl and members of MITgcm’s model development team, with particular help from Jean-Michel Campin, Kaspi has augmented the non-hydrostatic version of MITgcm so that the grid can reach deep in to a planet’s interior enabling consideration of a whole sphere of gas rather than just a shallow spherical shell.
Features of MITjcm (the MIT Jupiter Circulation Model) include:
- it is non-hydrostatic
- it has deep spherical geometry
- it is non-Boussinesq – Anelastic
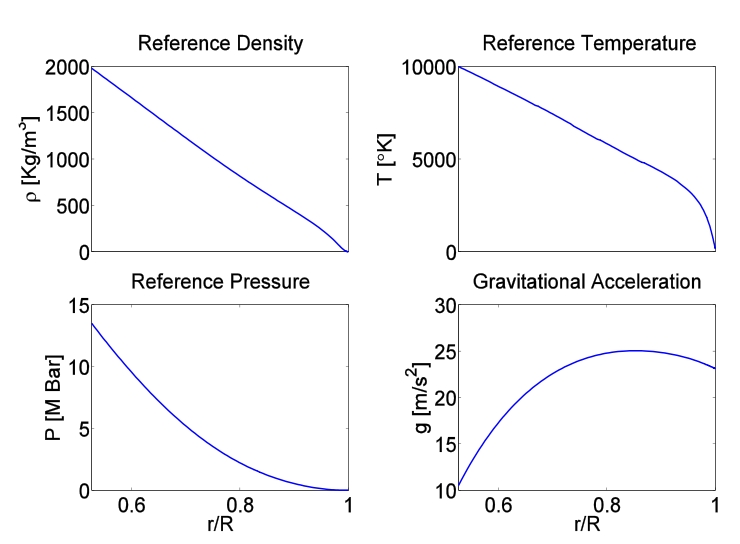
- it accomodates varying gravitational acceleration
- it incorporates a Hydrogen-Helium equation of state, (SCVH EOS) (Saumon et al. 1995)
- forcing is by interior and solar heat fluxes
Model Thermodynamics
Constituent gases are principally hydrogen and helium with small amounts of heavier elements. At low temperatures and pressures in the outer regions of the planet, hydrogen is a molecular gas and the EOS can be approximated as an ideal gas. Deeper into the interior, however, due to their high densities and relatively low temperatures (compared to stars), the giant planets lie in an extremely complex thermodynamic regime. The main factors that separate the gas under these conditions from ideal gas behavior are pressure, ionization, electron degeneracy, and Coulomb interactions.
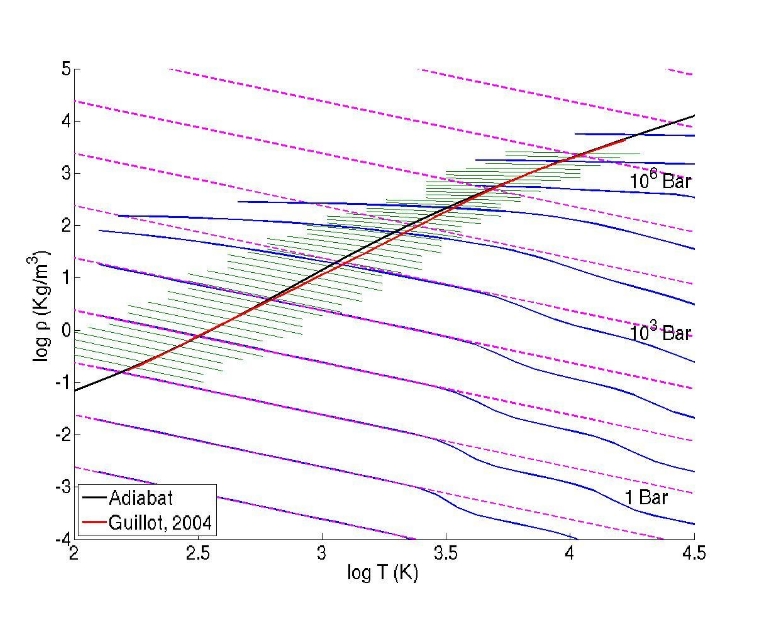
Figure 1: The SCVH EOS pressure contours (blue), ideal gas pressure contours (pink) and the adiabatic reference state (black). Model layers are in green. (image source - Yohai Kaspi)
Using the SCVH EOS (Saumon et al. 1995), calculated specifically for high pressure hydrogen and helium mixtures including these thermodynamic complexities, the pressure-temperature-density relationship for the model is as shown in Figure 1.
For the dynamical equations to remain energetically consistent when incorporating the anelastic approximation the system must have an adiabatic reference state (Figure 2). Kaspi uses the adiabat that matches Gallileo probe measurements (Atkinson et al., 1996). Variations from this reference entropy are computed dynamically. For more details see Kaspi et al, 2009…
Model Circulation
The movie below shows the evolution of the surface zonal velocity at the 1 bar pressure level. Using a simplified barotropic annulus configuration to study the interior dynamics of the system, Kaspi shows that the superrotating equatorial flow is driven by eddy angular momentum flux divergence due to radial variations in planetary vorticity.
The potential temperature anomaly is higher at the poles due to the alignment of the convective plumes with the rotation axis. Analysis of the heat budget shows that the poleward transfer of heat is mainly due to the eddy heat fluxes. This mechanism transfers heat poleward which may then balance the solar heating resulting in a weaker atmospheric meridional temperature gradient. The movie below shows the evolution of the entropy anomaly on the equatorial plane. Red represents higher entropy. The overlaid arrows indicate the associated velocity field.
Since the Rossby number is small and the system is convective the motion tends to align with the direction of the axis of rotation. Due to the mean density gradient the zonal velocities are stronger near the upper levels. The zonal velocities exhibit strong superrotation at low latitudes, with a weak flow in the opposite sense in the interior. Embedded in this shear are large positive vorticity columnular eddies.
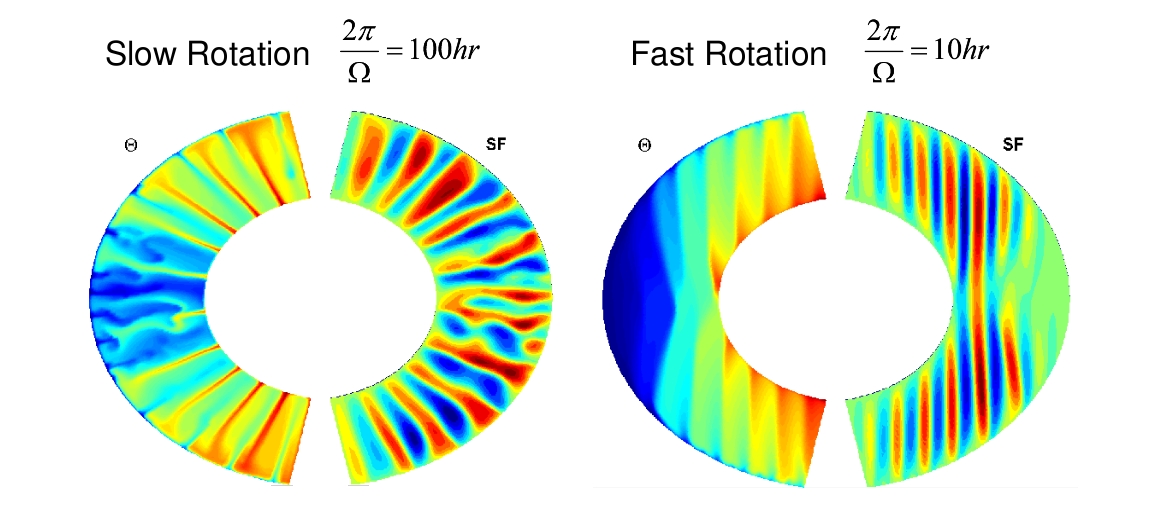
The Effect of Rotation
The system is convective and therefore plumes are driven by buoyancy away from the center of gravity. However since the Rossby number is small the convective motion tends to align with the axis of rotation. The ratio between the magnitude of the buoyancy frequency and the rotation frequency sets the degree of this alignment. The movies below compare two identical experiments which vary only in their rotation frequency. The more rapidly rotating experiment (the second movie) has convective motion aligned with the rotation axis while the more slowly rotating experiment (the movie immediately below) has a more homogeneous distribution of plumes. Both runs lie well into the turbulent regime (the Rayleigh number is around 100 times the critical value). After an initial period of spin up both runs are observed to reach a statistical steady state punctuated by sporadic plume emergence. The movies are of meridional entropy slices (radius – latitude). Brighter colors indicate higher entropy.
Figure 3 below shows the magnitude of the equatorial superrotation as function of the planetary rotation period (red), when looking at a set of experiments ranging from a rotation period of 2 hours to a rotation period of 200 hours. It shows that as the rotation period grows the flow switches from superrotation at the equator (eastward flow) to subrotation (westward flow). For Jupiter parameters the transition happens at a rotation period of about 60 hours. The reason for the regime transition is that when the rotation is fast enough the convection columns drive an eddy momentum flux outward near the equator which forces the superrotation (more details in Kaspi, 2008). The modified Rayleigh number (blue) gives us a scaling estimate for the magnitude and direction of the flow.
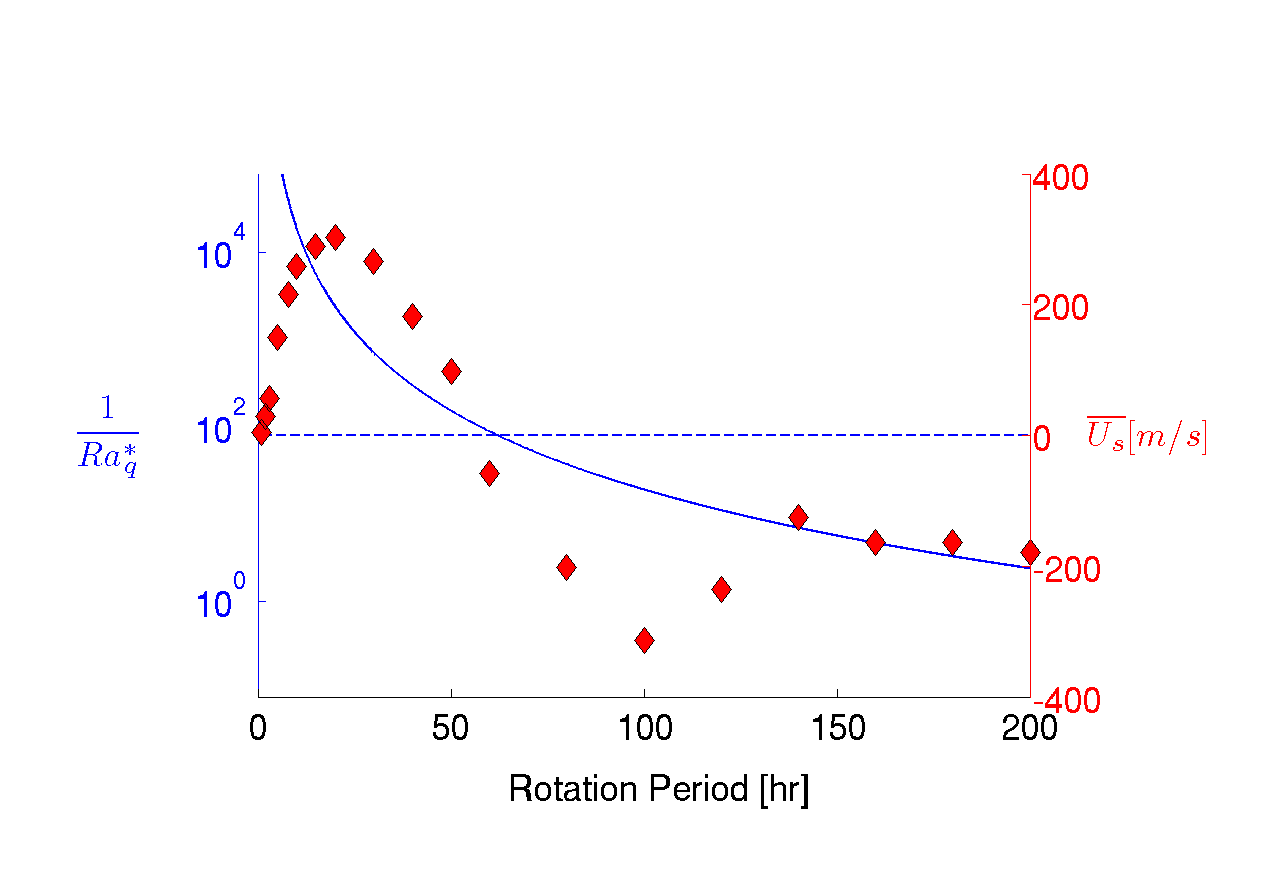
Figure 3: The zonally averaged zonal velocity at the 1 bar surface (red) and a modified Rayleigh number Ra*_q = Ra_q Ek^3 Pr^-2 (blue) as a function of rotation period for a set of experiments with equal parameters but varying rotation. (Image source - Yohai Kaspi)
One of the key questions on the giant planet’s atmospheres is what is the baroclinic structure of the zonal winds. If the flow would have been completely barotropic then the convective columns are expected to behave as Taylor columns and thus have no shear in the direction of the axis of rotation. However since this fluid has a large density variation from the atmosphere to the interior (varying from a fluid with 0.1 the density of air at 1 bar to twice the density of water at 1 Mbar), the flow develops a shear along the direction of the axis of rotation. Figure 4 below compares the zonal winds in a Boussinesq case (constant density) to an anelastic case (vertically varying density), showing the alignment of the zonal winds with the axis of rotation, where in the Boussinesq case the winds are constant while in the anelastic case the winds vary with depth.
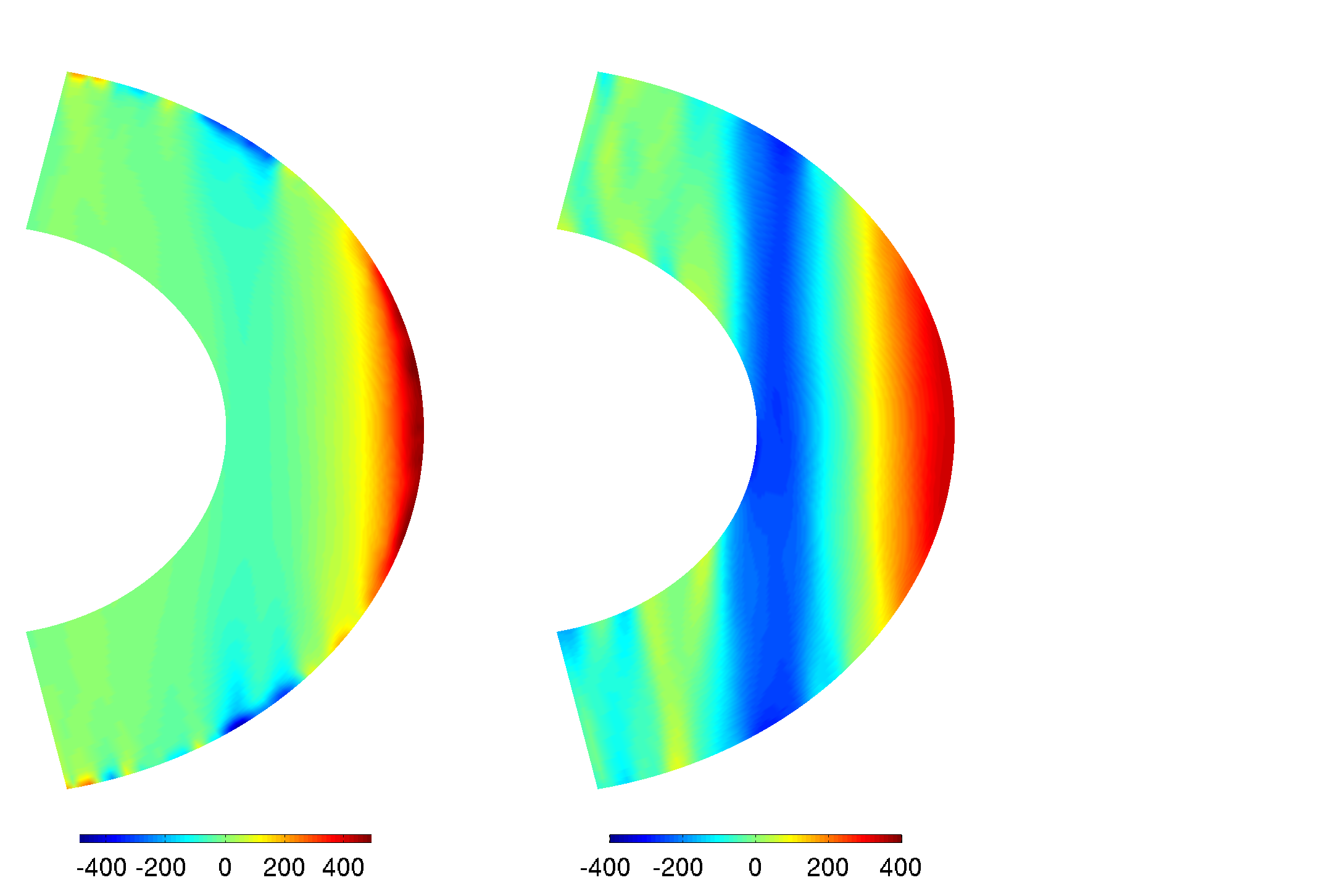
Figure 4: The zonally averaged zonal velocity (ms-1) for an anelastic run (left) and a Boussinesq run (right). Runs differ in Rayleigh number: Ra_q = 3 x 10^8 for anelastic and 1 x 10^9 for Boussinesq. Ekman and Prandtl numbers are equal in both runs: Ek =1.5 x 10^-4 and Pr = 10. (image source - Yohai Kaspi)
The Effect of Solar Forcing
To study the interaction between flow driven by internal convection and the flow resulting from exterior solar forcing, Kaspi introduced a shallow surface zone within which he could model absorption of solar heat flux. The plot on the right of Figure 5 below shows the 2D stream function (left hand panel) and zonal transport (right hand panel) where there is only solar forcing. With solar forcing alone, a meridional Hadley cell is created extending all the way to the pole. To the left of Figure 5 are comparable fields from an experiment which includes both interior and solar forcing. In this case the development of convection columns (constrained to high latitudes by anelastic effects) can be seen to interact with the Hadley circulation breaking it up into multiple smaller cells.
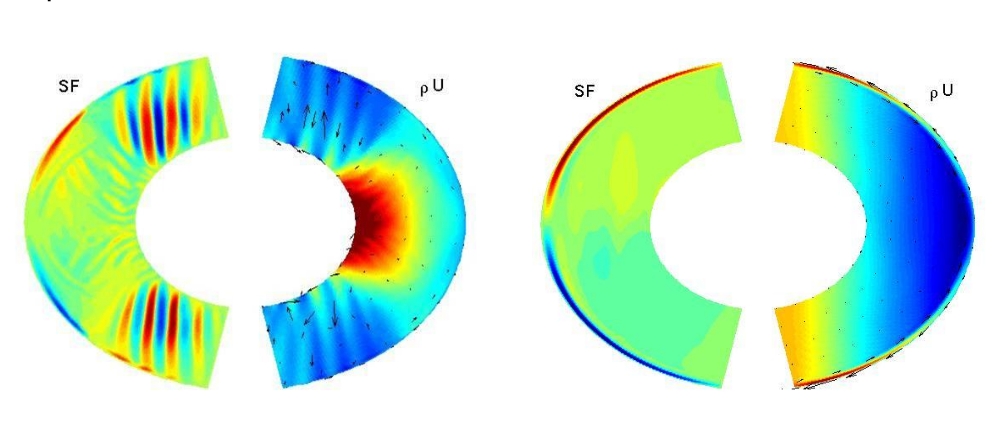
Figure 5: The Effect of Solar Forcing. Only solar (right) and both interior and solar (left) experiments. The left panels are the 2D stream function (with the r - latitude plane velocities in the superimposed arrows), and the right panels are the zonal transport. (image source - Yohai Kaspi)
Want to find out more? Contact Yohai.
References
Atkinson, D.H., J.B. Polack and A.Seiff (1985) Galileo Doppler Measurements of the Deep Zonal Winds of Jupiter, Science, 272, 842-843
Saumon D., G. Charbier and H.H. Van-Horn (1995) An EOS for Low Mass Stars and Giant Planets, Astrophys. J., 99, 713-741
Publications
Showman, A. P., Y. Kaspi and G. R. Flierl, 2010 Scaling laws for convection and jet speeds in giant planets (submitted)
Kaspi, Y., W. B. Hubbard, A. P. Showman and G. R. Flierl, 2010 The gravitational signature of Jupiter’s internal dynamics , Geophysical Review Letters, Vol. 37, L01204
Kaspi, Y., G. R. Flierl and A. P. Showman (2009) The deep wind structure of the giant planets: Results from an anelastic general circulation model, Icarus, 2002, 525-542
Kaspi, Y (2008) Turbulent convection in an anelastic rotating sphere: A model for the circulation on the giant planets, Ph.D Thesis, MIT-WHOI joint program, 2008).