• 6.4.5.1 Introduction
• 6.4.5.2 KL10 configuration and compiling
• 6.4.5.3 Run-time parameters
  • 6.4.5.3.1 Enabling the package
  • 6.4.5.3.2 Required MITgcm flags
  • 6.4.5.3.3 Package flags and parameters
  
  
• 6.4.5.4 Equations and key routines
  • 6.4.5.4.1 KL10_CALC:
  • 6.4.5.4.2 KL10_CALC_VISC:
  • 6.4.5.4.3 KL10_CALC_DIFF:
  
  
• 6.4.5.5 KL10 diagnostics
• 6.4.5.6 References
• 6.4.5.7 Experiments and tutorials that use KL10

6.4.5 KL10: Vertical Mixing Due to Breaking Internal Waves

Authors: Jody M. Klymak

6.4.5.1 Introduction

The Klymak and Legg [2010, KL10] parameterization for breaking internal waves is meant to represent mixing in the ocean ``interior'' due to convective instability. Many mixing schemes in the presence of unstable stratification simply turn on an arbitrarily large diffusivity and viscosity in the overturning region. This assumes the fluid completely mixes, which is probably not a terrible assumption, but it also makes estimating the turbulence dissipation rate in the overturning region meaningless.

The KL10 scheme overcomes this limitation by estimating the viscosity and diffusivity from a combination of the Ozmidov relation and the Osborn relation, assuming a turbulent Prandtl number of one. The Ozmidov relation says that outer scale of turbulence in an overturn will scale with the strength of the turbulence , and the stratification , as

(6.26)

(6.27)

(6.28)

The ocean turbulence community often approximates the Ozmidov scale by the root-mean-square of the Thorpe displacement, , in an overturn [Thorpe, 1977]. The Thorpe displacement is the distance one would have to move a water parcel for the water column to be stable, and is readily measured in a measured profile by sorting the profile and tracking how far each parcel moves during the sorting procedure. This method gives an imperfect estimate of the turbulence, but it has been found to agree on average over a large range of overturns [Moum, 1996; Seim and Gregg, 1994; Wesson and Gregg, 1994].

The algorithm coded here is a slight simplification of the usual Thorpe method for estimating turbulence in overturning regions. Usually, overturns are identified and is averaged over the overturn. Here, instead we estimate

(6.29)

We assume a turbulent Prandtl number of 1, so .

We also calculate and output a turbulent dissipation from this scheme. We do not simply evaluate the overturns for using (6.26). Instead we compute the vertical shear terms that the viscosity is acting on:

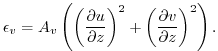(6.30)

There are straightforward caveats to this approach, covered in Klymak and Legg [2010].

• If your resolution is too low to resolve the breaking internal waves, you won't have any turbulence.
• If the model resolution is too high, the estimates of 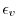will start to be exaggerated, particularly if the run in non-hydrostatic. That is because there will be significant shear at small scales that represents the turbulence being parameterized in the scheme. At very high resolutions direct numerical simulation or more sophisticated large-eddy schemes should be used.
• We find that grid cells of approximately 10 to 1 aspect ratio are a good rule of thumb for achieving good results are usual oceanic scales. For a site like the Hawaiian Ridge, and Luzon Strait, this means 10-m vertical resolusion and approximately 100-m horizontal. The 10-m resolution can be relaxed if the stratification drops, and we often WKB-stretch the grid spacing with depth.
• The dissipation estimate is useful for pinpoiting the location of turbulence, but again, is grid size dependent to some extent, and should be treated with a grain of salt. It will also not include any numerical dissipation such as you may find with higher order advection schemes.

6.4.5.2 KL10 configuration and compiling

As with all MITgcm packages, KL10 can be turned on or off at compile time

• using the packages.conf file by adding kl10 to it,
• or using genmake2 adding -enable=kl10 or -disable=kl10 switches
• Required packages and CPP options:
  No additional packages are required.

KL10 has no compile-time options (KL10_OPTIONS.h is empty).

6.4.5.3 Run-time parameters

Run-time parameters are set in files data.pkg and data.kl10 which are read in kl10_readparms.F. Run-time parameters may be broken into 3 categories: (i) switching on/off the package at runtime, (ii) required MITgcm flags, (iii) package flags and parameters.

6.4.5.3.1 Enabling the package

6.4.5.3.2 Required MITgcm flags

implicitViscosity = .TRUE.	enable implicit vertical viscosity
implicitDiffusion = .TRUE.	enable implicit vertical diffusion

6.4.5.3.3 Package flags and parameters

Table 6.8: KL10 runtime parameters

Flag/parameter default Description I/O related parameters KLviscMax 300 Maximum viscosity the scheme will ever give (useful for stability) KLdumpFreq dumpFreq Dump frequency of KL10 field snapshots KLtaveFreq taveFreq Averaging and dump frequency of KL10 fields KLwriteState .FALSE. write KL10 state to file

6.4.5.4 Equations and key routines

6.4.5.4.1 KL10_CALC:

6.4.5.4.2 KL10_CALC_VISC:

6.4.5.4.3 KL10_CALC_DIFF:

6.4.5.5 KL10 diagnostics

Diagnostics output is available via the diagnostics package (see Section 7.1). Available output fields are summarized here:

------------------------------------------------------
 <-Name->|Levs|grid|<--  Units   -->|<- Tile (max=80c)
------------------------------------------------------
 KLviscAr| Nr |SM  |m^2/s           |KL10 vertical eddy viscosity coefficient
 KLdiffKr| Nr |SM  |m^2/s           |Vertical diffusion coefficient for salt, temperature, & tracers
 KLeps  | Nr |SM  |m^3/s^3           | Turbulence dissipation estimate.

subsubsectionReference experiments

internal_wavekl10:

6.4.5.6 References

Klymak and Legg, 2010, Oc. Modell..

6.4.5.7 Experiments and tutorials that use KL10

• Modified Internal Wave experiment, in internal_wave verification directory

Copyright © 2006 Massachusetts Institute of Technology

Last update 2018-01-23