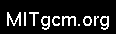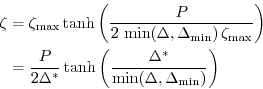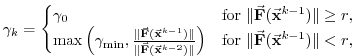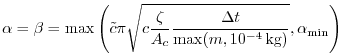Home Contact Us Site Map  
 
       
    next up previous contents
Next: 6.6.3 SHELFICE Package Up: 6.6 Sea Ice Packages Previous: 6.6.1 THSICE: The Thermodynamic   Contents

Subsections


6.6.2 SEAICE Package

Authors: Martin Losch, Dimitris Menemenlis, An Nguyen, Jean-Michel Campin, Patrick Heimbach, Chris Hill and Jinlun Zhang


6.6.2.1 Introduction

Package ``seaice'' provides a dynamic and thermodynamic interactive sea-ice model.

CPP options enable or disable different aspects of the package (Section 6.6.2.2). Run-Time options, flags, filenames and field-related dates/times are set in data.seaice (Section 6.6.2.3). A description of key subroutines is given in Section 6.6.2.5. Input fields, units and sign conventions are summarized in Section 6.6.2.3, and available diagnostics output is listed in Section 6.6.2.6.

6.6.2.2 SEAICE configuration, compiling & running


6.6.2.2.1 Compile-time options

 

As with all MITgcm packages, SEAICE can be turned on or off at compile time

  • using the packages.conf file by adding seaice to it,
  • or using genmake2 adding -enable=seaice or -disable=seaice switches
  • required packages and CPP options:
    SEAICE requires the external forcing package exf to be enabled; no additional CPP options are required.
(see Section 3.4).

Parts of the SEAICE code can be enabled or disabled at compile time via CPP preprocessor flags. These options are set in SEAICE_OPTIONS.h. Table 6.6.2.2 summarizes the most important ones. For more options see the default pkg/seaice/SEAICE_OPTIONS.h.


Table 6.18: Some of the most relevant CPP preprocessor flags in the seaice-package.
CPP option Description
SEAICE_DEBUG Enhance STDOUT for debugging
SEAICE_ALLOW_DYNAMICS sea-ice dynamics code
SEAICE_CGRID LSR solver on C-grid (rather than original B-grid)
SEAICE_ALLOW_EVP enable use of EVP rheology solver
SEAICE_ALLOW_JFNK enable use of JFNK rheology solver
SEAICE_EXTERNAL_FLUXES use EXF-computed fluxes as starting point
SEAICE_ZETA_SMOOTHREG use differentialable regularization for viscosities
SEAICE_VARIABLE_FREEZING_POINT enable linear dependence of the freezing point on salinity (by default undefined)
ALLOW_SEAICE_FLOODING enable snow to ice conversion for submerged sea-ice
SEAICE_VARIABLE_SALINITY enable sea-ice with variable salinity (by default undefined)
SEAICE_SITRACER enable sea-ice tracer package (by default undefined)
SEAICE_BICE_STRESS B-grid only for backward compatiblity: turn on ice-stress on ocean
EXPLICIT_SSH_SLOPE B-grid only for backward compatiblity: use ETAN for tilt computations rather than geostrophic velocities



6.6.2.3 Run-time parameters

Run-time parameters (see Table 6.19) are set in files data.pkg (read in packages_readparms.F), and data.seaice (read in seaice_readparms.F).

6.6.2.3.1 Enabling the package

 
A package is switched on/off at run-time by setting (e.g. for SEAICE) useSEAICE = .TRUE. in data.pkg.

6.6.2.3.2 General flags and parameters

 
Table 6.19 lists most run-time parameters.


Table 6.19: Run-time parameters and default values
Name Default value Description Reference
SEAICEwriteState T write sea ice state to file
SEAICEuseDYNAMICS T use dynamics
SEAICEuseJFNK F use the JFNK-solver
SEAICEuseTEM F use truncated ellipse method
SEAICEuseStrImpCpl F use strength implicit coupling in LSR/JFNK
SEAICEuseMetricTerms T use metric terms in dynamics
SEAICEuseEVPpickup T use EVP pickups
SEAICEuseFluxForm F use flux form for 2nd central difference advection scheme
SEAICErestoreUnderIce F enable restoring to climatology under ice
useHB87stressCoupling F turn on ice-ocean stress coupling following Hibler and Bryan [1987]
usePW79thermodynamics T flag to turn off zero-layer-thermodynamics for testing
SEAICEadvHeff/Area/Snow/Salt T flag to turn off advection of scalar state variables
SEAICEuseFlooding T use flood-freeze algorithm
SEAICE_no_slip F switch between free-slip and no-slip boundary conditions
SEAICE_deltaTtherm dTracerLev(1) thermodynamic timestep
SEAICE_deltaTdyn dTracerLev(1) dynamic timestep
SEAICE_deltaTevp 0 EVP sub-cycling time step, values $ >$ 0 turn on EVP
SEAICEuseEVPstar F use modified EVP* instead of EVP
SEAICEuseEVPrev F use yet another variation on EVP*
SEAICEnEVPstarSteps UNSET number of modified EVP* iteration
SEAICE_evpAlpha UNSET EVP* parameter
SEAICE_evpBeta UNSET EVP* parameter
SEAICEaEVPcoeff UNSET aEVP parameter
SEAICEaEVPcStar 4 aEVP parameter [Kimmritz et al., 2016]
SEAICEaEVPalphaMin 5 aEVP parameter [Kimmritz et al., 2016]
SEAICE_elasticParm $ \frac{1}{3}$ EVP paramter $ E_0$
SEAICE_evpTauRelax $ \Delta{t}_{EVP}E_0$ relaxation time scale $ T$ for EVP waves
SEAICEnewtonIterMax 10 maximum number of JFNK-Newton iterations
SEAICEkrylovIterMax 10 maximum number of JFNK-Krylov iterations
SEAICE_JFNK_lsIter (off) start line search after ``lsIter'' Newton iterations
JFNKgamma_nonlin 1.0E-05 non-linear tolerance parameter for JFNK solver
JFNKgamma_lin_min/max 0.10/0.99 tolerance parameters for linear JFNK solver
JFNKres_tFac UNSET tolerance parameter for FGMRES residual
SEAICE_JFNKepsilon 1.0E-06 step size for the FD-Jacobian-times-vector
SEAICE_dumpFreq dumpFreq dump frequency
SEAICE_taveFreq taveFreq time-averaging frequency
SEAICE_dump_mdsio T write snap-shot using MDSIO
SEAICE_tave_mdsio T write TimeAverage using MDSIO
SEAICE_dump_mnc F write snap-shot using MNC
SEAICE_tave_mnc F write TimeAverage using MNC
SEAICE_initialHEFF 0.00000E+00 initial sea-ice thickness
SEAICE_drag 2.00000E-03 air-ice drag coefficient
OCEAN_drag 1.00000E-03 air-ocean drag coefficient
SEAICE_waterDrag 5.50000E+00 water-ice drag
SEAICE_dryIceAlb 7.50000E-01 winter albedo
SEAICE_wetIceAlb 6.60000E-01 summer albedo
SEAICE_drySnowAlb 8.40000E-01 dry snow albedo
SEAICE_wetSnowAlb 7.00000E-01 wet snow albedo
SEAICE_waterAlbedo 1.00000E-01 water albedo
SEAICE_strength 2.75000E+04 sea-ice strength $ P^{*}$
SEAICE_cStar 20.0000E+00 sea-ice strength paramter $ C^{*}$
SEAICE_rhoAir 1.3 (or exf value) density of air (kg/m$ ^3$ )
SEAICE_cpAir 1004 (or exf value) specific heat of air (J/kg/K)
SEAICE_lhEvap 2,500,000 (or exf value) latent heat of evaporation
SEAICE_lhFusion 334,000 (or exf value) latent heat of fusion
SEAICE_lhSublim 2,834,000 latent heat of sublimation
SEAICE_dalton 1.75E-03 sensible heat transfer coefficient
SEAICE_iceConduct 2.16560E+00 sea-ice conductivity
SEAICE_snowConduct 3.10000E-01 snow conductivity
SEAICE_emissivity 5.50000E-08 Stefan-Boltzman
SEAICE_snowThick 1.50000E-01 cutoff snow thickness
SEAICE_shortwave 3.00000E-01 penetration shortwave radiation
SEAICE_freeze -1.96000E+00 freezing temp. of sea water
SEAICE_saltFrac 0.0 salinity newly formed ice (fraction of ocean surface salinity)
SEAICE_frazilFrac 0.0 Fraction of surface level negative heat content anomalies (relative to the local freezing point)
SEAICEstressFactor 1.00000E+00 scaling factor for ice-ocean stress
Heff/Area/HsnowFile/Hsalt UNSET initial fields for variables HEFF/AREA/HSNOW/HSALT
LSR_ERROR 1.00000E-04 sets accuracy of LSR solver
DIFF1 0.0 parameter used in advect.F
HO 5.00000E-01 demarcation ice thickness (AKA lead closing paramter $ h_0$ )
MAX_HEFF 1.00000E+01 maximum ice thickness
MIN_ATEMP -5.00000E+01 minimum air temperature
MIN_LWDOWN 6.00000E+01 minimum downward longwave
MAX_TICE 3.00000E+01 maximum ice temperature
MIN_TICE -5.00000E+01 minimum ice temperature
IMAX_TICE 10 iterations for ice heat budget
SEAICE_EPS 1.00000E-10 reduce derivative singularities
SEAICE_area_reg 1.00000E-5 minimum concentration to regularize ice thickness
SEAICE_hice_reg 0.05 m minimum ice thickness for regularization
SEAICE_multDim 1 number of ice categories for thermodynamics
SEAICE_useMultDimSnow F use SEAICE_multDim snow categories


6.6.2.3.3 Input fields and units

HeffFile:
Initial sea ice thickness averaged over grid cell in meters; initializes variable HEFF;
AreaFile:
Initial fractional sea ice cover, range $ [0,1]$ ; initializes variable AREA;
HsnowFile:
Initial snow thickness on sea ice averaged over grid cell in meters; initializes variable HSNOW;
HsaltFile:
Initial salinity of sea ice averaged over grid cell in g/m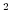$ ^2$ ; initializes variable HSALT;


6.6.2.4 Description

[TO BE CONTINUED/MODIFIED]

The MITgcm sea ice model (MITgcm/sim) is based on a variant of the viscous-plastic (VP) dynamic-thermodynamic sea ice model [Zhang and Hibler, 1997] first introduced by Hibler [1980,1979]. In order to adapt this model to the requirements of coupled ice-ocean state estimation, many important aspects of the original code have been modified and improved [Losch et al., 2010]:

  • the code has been rewritten for an Arakawa C-grid, both B- and C-grid variants are available; the C-grid code allows for no-slip and free-slip lateral boundary conditions;
  • three different solution methods for solving the nonlinear momentum equations have been adopted: LSOR [Zhang and Hibler, 1997], EVP [Hunke and Dukowicz, 1997], JFNK [Losch et al., 2014; Lemieux et al., 2010];
  • ice-ocean stress can be formulated as in Hibler and Bryan [1987] or as in Campin et al. [2008];
  • ice variables are advected by sophisticated, conservative advection schemes with flux limiting;
  • growth and melt parameterizations have been refined and extended in order to allow for more stable automatic differentiation of the code.
The sea ice model is tightly coupled to the ocean compontent of the MITgcm. Heat, fresh water fluxes and surface stresses are computed from the atmospheric state and - by default - modified by the ice model at every time step.

The ice dynamics models that are most widely used for large-scale climate studies are the viscous-plastic (VP) model [Hibler, 1979], the cavitating fluid (CF) model [Flato and Hibler, 1992], and the elastic-viscous-plastic (EVP) model [Hunke and Dukowicz, 1997]. Compared to the VP model, the CF model does not allow ice shear in calculating ice motion, stress, and deformation. EVP models approximate VP by adding an elastic term to the equations for easier adaptation to parallel computers. Because of its higher accuracy in plastic solution and relatively simpler formulation, compared to the EVP model, we decided to use the VP model as the default dynamic component of our ice model. To do this we extended the line successive over relaxation (LSOR) method of Zhang and Hibler [1997] for use in a parallel configuration. An EVP model and a free-drift implemtation can be selected with runtime flags.


6.6.2.4.1 Compatibility with ice-thermodynamics package thsice

 
Note, that by default the seaice-package includes the orginial so-called zero-layer thermodynamics following Hibler [1980] with a snow cover as in Zhang et al. [1998]. The zero-layer thermodynamic model assumes that ice does not store heat and, therefore, tends to exaggerate the seasonal variability in ice thickness. This exaggeration can be significantly reduced by using Semtner's [1976] three-layer thermodynamic model that permits heat storage in ice. Recently, the three-layer thermodynamic model has been reformulated by Winton [2000]. The reformulation improves model physics by representing the brine content of the upper ice with a variable heat capacity. It also improves model numerics and consumes less computer time and memory.

The Winton sea-ice thermodynamics have been ported to the MIT GCM; they currently reside under pkg/thsice. The package thsice is described in section 6.6.1; it is fully compatible with the packages seaice and exf. When turned on together with seaice, the zero-layer thermodynamics are replaced by the Winton thermodynamics. In order to use the seaice-package with the thermodynamics of thsice, compile both packages and turn both package on in data.pkg; see an example in global_ocean.cs32x15/input.icedyn. Note, that once thsice is turned on, the variables and diagnostics associated to the default thermodynamics are meaningless, and the diagnostics of thsice have to be used instead.


6.6.2.4.2 Surface forcing

 
The sea ice model requires the following input fields: 10-m winds, 2-m air temperature and specific humidity, downward longwave and shortwave radiations, precipitation, evaporation, and river and glacier runoff. The sea ice model also requires surface temperature from the ocean model and the top level horizontal velocity. Output fields are surface wind stress, evaporation minus precipitation minus runoff, net surface heat flux, and net shortwave flux. The sea-ice model is global: in ice-free regions bulk formulae are used to estimate oceanic forcing from the atmospheric fields.


6.6.2.4.3 Dynamics

 
The momentum equation of the sea-ice model is

$\displaystyle m \frac{D\ensuremath{\vec{\mathbf{u}}}}{Dt} = -mf\ensuremath{\vec... ...f{\mathbf{\tau}}}}_{ocean} - m \nabla{\phi(0)} + \ensuremath{\vec{\mathbf{F}}},$ (6.39)

where $ m=m_{i}+m_{s}$ is the ice and snow mass per unit area; $ \ensuremath{\vec{\mathbf{u}}}=u\ensuremath{\vec{\mathbf{i}}}+v\ensuremath{\vec{\mathbf{j}}}$ is the ice velocity vector; $ \ensuremath{\vec{\mathbf{i}}}$ , $ \ensuremath{\vec{\mathbf{j}}}$ , and $ \ensuremath{\vec{\mathbf{k}}}$ are unit vectors in the $ x$ , $ y$ , and $ z$ directions, respectively; $ f$ is the Coriolis parameter; $ \ensuremath{\vec{\mathbf{\mathbf{\tau}}}}_{air}$ and $ \ensuremath{\vec{\mathbf{\mathbf{\tau}}}}_{ocean}$ are the wind-ice and ocean-ice stresses, respectively; $ g$ is the gravity accelation; $ \nabla\phi(0)$ is the gradient (or tilt) of the sea surface height; $ \phi(0) = g\eta + p_{a}/\rho_{0} + mg/\rho_{0}$ is the sea surface height potential in response to ocean dynamics ($ g\eta$ ), to atmospheric pressure loading ( $ p_{a}/\rho_{0}$ , where $ \rho_{0}$ is a reference density) and a term due to snow and ice loading [Campin et al., 2008]; and $ \ensuremath{\vec{\mathbf{F}}}=\nabla\cdot\sigma$ is the divergence of the internal ice stress tensor $ \sigma_{ij}$ . Advection of sea-ice momentum is neglected. The wind and ice-ocean stress terms are given by

$\displaystyle \ensuremath{\vec{\mathbf{\mathbf{\tau}}}}_{air} =$ $\displaystyle \rho_{air} C_{air} \vert\ensuremath{\vec{\mathbf{U}}}_{air} -\ens... ...t R_{air} (\ensuremath{\vec{\mathbf{U}}}_{air} -\ensuremath{\vec{\mathbf{u}}}),$    
$\displaystyle \ensuremath{\vec{\mathbf{\mathbf{\tau}}}}_{ocean} =$ $\displaystyle \rho_{ocean}C_{ocean} \vert\ensuremath{\vec{\mathbf{U}}}_{ocean}-... ...R_{ocean}(\ensuremath{\vec{\mathbf{U}}}_{ocean}-\ensuremath{\vec{\mathbf{u}}}),$    

where $ \ensuremath{\vec{\mathbf{U}}}_{air/ocean}$ are the surface winds of the atmosphere and surface currents of the ocean, respectively; $ C_{air/ocean}$ are air and ocean drag coefficients; $ \rho_{air/ocean}$ are reference densities; and $ R_{air/ocean}$ are rotation matrices that act on the wind/current vectors.


6.6.2.4.4 Viscous-Plastic (VP) Rheology

 
For an isotropic system the stress tensor $ \sigma_{ij}$ ($ i,j=1,2$ ) can be related to the ice strain rate and strength by a nonlinear viscous-plastic (VP) constitutive law [Hibler, 1979; Zhang and Hibler, 1997]:

$\displaystyle \sigma_{ij}=2\eta(\dot{\epsilon}_{ij},P)\dot{\epsilon}_{ij} + \le... ...epsilon}_{ij},P)\right]\dot{\epsilon}_{kk}\delta_{ij} - \frac{P}{2}\delta_{ij}.$ (6.40)

The ice strain rate is given by

$\displaystyle \dot{\epsilon}_{ij} = \frac{1}{2}\left( \frac{\partial{u_{i}}}{\partial{x_{j}}} + \frac{\partial{u_{j}}}{\partial{x_{i}}}\right).$    

The maximum ice pressure $ P_{\max}$ , a measure of ice strength, depends on both thickness $ h$ and compactness (concentration) $ c$ :

$\displaystyle P_{\max} = P^{*}c\,h\,\exp\{-C^{*}\cdot(1-c)\},$ (6.41)

with the constants $ P^{*}$ (run-time parameter SEAICE_strength) and $ C^{*}=20$ . The nonlinear bulk and shear viscosities $ \eta $ and $ \zeta$ are functions of ice strain rate invariants and ice strength such that the principal components of the stress lie on an elliptical yield curve with the ratio of major to minor axis $ e$ equal to $ 2$ ; they are given by:

$\displaystyle \zeta =$ $\displaystyle \min\left(\frac{P_{\max}}{2\max(\Delta,\Delta_{\min})}, \zeta_{\max}\right)$    
$\displaystyle \eta =$ $\displaystyle \frac{\zeta}{e^2}$    

with the abbreviation


$\displaystyle \Delta =$ $\displaystyle \left[ \left(\dot{\epsilon}_{11}^2+\dot{\epsilon}_{22}^2\right) (... ...}^2 + 2\dot{\epsilon}_{11}\dot{\epsilon}_{22} (1-e^{-2}) \right]^{\frac{1}{2}}.$    

The bulk viscosities are bounded above by imposing both a minimum $ \Delta_{\min}$ (for numerical reasons, run-time parameter SEAICE_EPS with a default value of $ 10^{-10}$ s$ ^{-1}$ ) and a maximum $ \zeta_{\max} = P_{\max}/\Delta^*$ , where $ \Delta^*=(5\times10^{12}/2\times10^4)$ s$ ^{-1}$ . (There is also the option of bounding $ \zeta$ from below by setting run-time parameter SEAICE_zetaMin $ >0$ , but this is generally not recommended). For stress tensor computation the replacement pressure $ P = 2\,\Delta\zeta$ [Hibler and Ip, 1995] is used so that the stress state always lies on the elliptic yield curve by definition.

Defining the CPP-flag SEAICE_ZETA_SMOOTHREG in SEAICE_OPTIONS.h before compiling replaces the method for bounding $ \zeta$ by a smooth (differentiable) expression:

\begin{displaymath}\begin{split}\zeta &= \zeta_{\max}\tanh\left(\frac{P}{2\,\min... ...(\frac{\Delta^*}{\min(\Delta,\Delta_{\min})}\right) \end{split}\end{displaymath} (6.42)

where $ \Delta_{\min}=10^{-20}$ s$ ^{-1}$ is chosen to avoid divisions by zero.


6.6.2.4.5 LSR and JFNK solver

 

In the matrix notation, the discretized momentum equations can be written as

$\displaystyle \ensuremath{\mathbf{A}}(\ensuremath{\vec{\mathbf{x}}})\,\ensurema... ...ec{\mathbf{x}}} = \ensuremath{\vec{\mathbf{b}}}(\ensuremath{\vec{\mathbf{x}}}).$ (6.43)

The solution vector $ \ensuremath{\vec{\mathbf{x}}}$ consists of the two velocity components $ u$ and $ v$ that contain the velocity variables at all grid points and at one time level. The standard (and default) method for solving Eq.(6.43) in the sea ice component of the MITgcm, as in many sea ice models, is an iterative Picard solver: in the $ k$ -th iteration a linearized form $ \ensuremath{\mathbf{A}}(\ensuremath{\vec{\mathbf{x}}}^{k-1})\,\ensuremath{\vec... ...f{x}}}^{k} = \ensuremath{\vec{\mathbf{b}}}(\ensuremath{\vec{\mathbf{x}}}^{k-1})$ is solved (in the case of the MITgcm it is a Line Successive (over) Relaxation (LSR) algorithm [Zhang and Hibler, 1997]). Picard solvers converge slowly, but generally the iteration is terminated after only a few non-linear steps [Lemieux and Tremblay, 2009; Zhang and Hibler, 1997] and the calculation continues with the next time level. This method is the default method in the MITgcm. The number of non-linear iteration steps or pseudo-time steps can be controlled by the runtime parameter NPSEUDOTIMESTEPS (default is 2).

In order to overcome the poor convergence of the Picard-solver, Lemieux et al. [2010] introduced a Jacobian-free Newton-Krylov solver for the sea ice momentum equations. This solver is also implemented in the MITgcm [Losch et al., 2014]. The Newton method transforms minimizing the residual $ \ensuremath{\vec{\mathbf{F}}}(\ensuremath{\vec{\mathbf{x}}}) = \ensuremath{\ma... ...vec{\mathbf{x}}} - \ensuremath{\vec{\mathbf{b}}}(\ensuremath{\vec{\mathbf{x}}})$ to finding the roots of a multivariate Taylor expansion of the residual $ \vec{\mathbf{F}}$ around the previous ($ k-1$ ) estimate $ \ensuremath{\vec{\mathbf{x}}}^{k-1}$ :

$\displaystyle \ensuremath{\vec{\mathbf{F}}}(\ensuremath{\vec{\mathbf{x}}}^{k-1}... ...'(\ensuremath{\vec{\mathbf{x}}}^{k-1})\,\delta\ensuremath{\vec{\mathbf{x}}}^{k}$ (6.44)

with the Jacobian $ \ensuremath{\mathbf{J}}\equiv\ensuremath{\vec{\mathbf{F}}}'$ . The root $ \ensuremath{\vec{\mathbf{F}}}(\ensuremath{\vec{\mathbf{x}}}^{k-1}+\delta\ensuremath{\vec{\mathbf{x}}}^{k})=0$ is found by solving

$\displaystyle \ensuremath{\mathbf{J}}(\ensuremath{\vec{\mathbf{x}}}^{k-1})\,\de... ...{x}}}^{k} = -\ensuremath{\vec{\mathbf{F}}}(\ensuremath{\vec{\mathbf{x}}}^{k-1})$ (6.45)

for $ \delta\ensuremath{\vec{\mathbf{x}}}^{k}$ . The next ($ k$ -th) estimate is given by $ \ensuremath{\vec{\mathbf{x}}}^{k}=\ensuremath{\vec{\mathbf{x}}}^{k-1}+a\,\delta\ensuremath{\vec{\mathbf{x}}}^{k}$ . In order to avoid overshoots the factor $ a$ is iteratively reduced in a line search ( $ a=1, \frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \ldots$ ) until $ \Vert\ensuremath{\vec{\mathbf{F}}}(\ensuremath{\vec{\mathbf{x}}}^k)\Vert < \Vert\ensuremath{\vec{\mathbf{F}}}(\ensuremath{\vec{\mathbf{x}}}^{k-1})\Vert$ , where $ \Vert\cdot\Vert=\int\cdot\,dx^2$ is the $ L_2$ -norm. In practice, the line search is stopped at $ a=\frac{1}{8}$ . The line search starts after $ \texttt{SEAICE\_JFNK\_lsIter}$ non-linear Newton iterations (off by default).

Forming the Jacobian $ \ensuremath{\mathbf{J}}$ explicitly is often avoided as ``too error prone and time consuming'' [Knoll and Keyes, 2004]. Instead, Krylov methods only require the action of $ \mathbf{J}$ on an arbitrary vector $ \vec{\mathbf{w}}$ and hence allow a matrix free algorithm for solving Eq.(6.45) [Knoll and Keyes, 2004]. The action of $ \mathbf{J}$ can be approximated by a first-order Taylor series expansion:

$\displaystyle \ensuremath{\mathbf{J}}(\ensuremath{\vec{\mathbf{x}}}^{k-1})\,\en... ... \ensuremath{\vec{\mathbf{F}}}(\ensuremath{\vec{\mathbf{x}}}^{k-1})} {\epsilon}$ (6.46)

or computed exactly with the help of automatic differentiation (AD) tools. SEAICE_JFNKepsilon sets the step size $ \epsilon$ .

We use the Flexible Generalized Minimum RESidual method [FGMRES, Saad, 1993] with right-hand side preconditioning to solve Eq.(6.45) iteratively starting from a first guess of $ \delta\ensuremath{\vec{\mathbf{x}}}^{k}_{0} = 0$ . For the preconditioning matrix $ \mathbf{P}$ we choose a simplified form of the system matrix $ \ensuremath{\mathbf{A}}(\ensuremath{\vec{\mathbf{x}}}^{k-1})$ [Lemieux et al., 2010] where $ \ensuremath{\vec{\mathbf{x}}}^{k-1}$ is the estimate of the previous Newton step $ k-1$ . The transformed equation(6.45) becomes

$\displaystyle \ensuremath{\mathbf{J}}(\ensuremath{\vec{\mathbf{x}}}^{k-1})\,\en... ...hbf{z}}} = -\ensuremath{\vec{\mathbf{F}}}(\ensuremath{\vec{\mathbf{x}}}^{k-1}),$   with$\displaystyle \quad \delta\ensuremath{\vec{\mathbf{z}}}=\ensuremath{\mathbf{P}}\delta\ensuremath{\vec{\mathbf{x}}}^{k}.$ (6.47)

The Krylov method iteratively improves the approximate solution to (6.47) in subspace ( $ \ensuremath{\vec{\mathbf{r}}}_0$ , $ \ensuremath{\mathbf{J}}\ensuremath{\mathbf{P}}^{-1}\ensuremath{\vec{\mathbf{r}}}_0$ , $ (\ensuremath{\mathbf{J}}\ensuremath{\mathbf{P}}^{-1})^2\ensuremath{\vec{\mathbf{r}}}_0$ , ..., $ (\ensuremath{\mathbf{J}}\ensuremath{\mathbf{P}}^{-1})^m\ensuremath{\vec{\mathbf{r}}}_0$ ) with increasing $ m$ ; $ \ensuremath{\vec{\mathbf{r}}}_0 = -\ensuremath{\vec{\mathbf{F}}}(\ensuremath{\... ...nsuremath{\vec{\mathbf{x}}}^{k-1})\,\delta\ensuremath{\vec{\mathbf{x}}}^{k}_{0}$ is the initial residual of (6.45); $ \ensuremath{\vec{\mathbf{r}}}_0=-\ensuremath{\vec{\mathbf{F}}}(\ensuremath{\vec{\mathbf{x}}}^{k-1})$ with the first guess $ \delta\ensuremath{\vec{\mathbf{x}}}^{k}_{0} = 0$ . We allow a Krylov-subspace of dimension $ m=50$ and we do not use restarts. The preconditioning operation involves applying $ \ensuremath{\mathbf{P}}^{-1}$ to the basis vectors $ \ensuremath{\vec{\mathbf{v}}}_0, \ensuremath{\vec{\mathbf{v}}}_1, \ensuremath{\vec{\mathbf{v}}}_2, \ldots, \ensuremath{\vec{\mathbf{v}}}_m$ of the Krylov subspace. This operation is approximated by solving the linear system $ \ensuremath{\mathbf{P}}\,\ensuremath{\vec{\mathbf{w}}}=\ensuremath{\vec{\mathbf{v}}}_i$ . Because $ \ensuremath{\mathbf{P}} \approx \ensuremath{\mathbf{A}}(\ensuremath{\vec{\mathbf{x}}}^{k-1})$ , we can use the LSR-algorithm [Zhang and Hibler, 1997] already implemented in the Picard solver. Each preconditioning operation uses a fixed number of 10 LSR-iterations avoiding any termination criterion. More details and results can be found in Losch et al. [2014]; Lemieux et al. [2010].

To use the JFNK-solver set SEAICEuseJFNK = .TRUE. in the namelist file data.seaice; SEAICE_ALLOW_JFNK needs to be defined in SEAICE_OPTIONS.h and we recommend using a smooth regularization of $ \zeta$ by defining SEAICE_ZETA_SMOOTHREG (see above) for better convergence. The non-linear Newton iteration is terminated when the $ L_2$ -norm of the residual is reduced by $ \gamma_{\mathrm{nl}}$ (runtime parameter JFNKgamma_nonlin = 1.e-4 will already lead to expensive simulations) with respect to the initial norm: $ \Vert\ensuremath{\vec{\mathbf{F}}}(\ensuremath{\vec{\mathbf{x}}}^k)\Vert < \ga... ...rm{nl}}\Vert\ensuremath{\vec{\mathbf{F}}}(\ensuremath{\vec{\mathbf{x}}}^0)\Vert$ . Within a non-linear iteration, the linear FGMRES solver is terminated when the residual is smaller than $ \gamma_k\Vert\ensuremath{\vec{\mathbf{F}}}(\ensuremath{\vec{\mathbf{x}}}^{k-1})\Vert$ where $ \gamma_k$ is determined by

$\displaystyle \gamma_k = \begin{cases}\gamma_0 &\text{for $\Vert\ensuremath{\ve... ...{\vec{\mathbf{F}}}(\ensuremath{\vec{\mathbf{x}}}^{k-1})\Vert < r$,} \end{cases}$ (6.48)

so that the linear tolerance parameter $ \gamma_k$ decreases with the non-linear Newton step as the non-linear solution is approached. This inexact Newton method is generally more robust and computationally more efficient than exact methods [e.g., Knoll and Keyes, 2004]. Typical parameter choices are $ \gamma_0=\texttt{JFNKgamma\_lin\_max}=0.99$ , $ \gamma_{\min}=\texttt{JFNKgamma\_lin\_min}=0.1$ , and $ r = \texttt{JFNKres\_tFac}\times\Vert\ensuremath{\vec{\mathbf{F}}}(\ensuremath{\vec{\mathbf{x}}}^{0})\Vert$ with $ \texttt{JFNKres\_tFac} = \frac{1}{2}$ . We recommend a maximum number of non-linear iterations $ \texttt{SEAICEnewtonIterMax} = 100$ and a maximum number of Krylov iterations $ \texttt{SEAICEkrylovIterMax} = 50$ , because the Krylov subspace has a fixed dimension of 50.

Setting SEAICEuseStrImpCpl = .TRUE., turns on ``strength implicit coupling'' [Hutchings et al., 2004] in the LSR-solver and in the LSR-preconditioner for the JFNK-solver. In this mode, the different contributions of the stress divergence terms are re-ordered in order to increase the diagonal dominance of the system matrix. Unfortunately, the convergence rate of the LSR solver is increased only slightly, while the JFNK-convergence appears to be unaffected.


6.6.2.4.6 Elastic-Viscous-Plastic (EVP) Dynamics

 
Hunke and Dukowicz [1997]'s introduced an elastic contribution to the strain rate in order to regularize Eq. 6.40 in such a way that the resulting elastic-viscous-plastic (EVP) and VP models are identical at steady state,

$\displaystyle \frac{1}{E}\frac{\partial\sigma_{ij}}{\partial{t}} + \frac{1}{2\e... ...eta}\sigma_{kk}\delta_{ij} + \frac{P}{4\zeta}\delta_{ij} = \dot{\epsilon}_{ij}.$ (6.49)

The EVP-model uses an explicit time stepping scheme with a short timestep. According to the recommendation of Hunke and Dukowicz [1997], the EVP-model should be stepped forward in time 120 times ( $ \texttt{SEAICE\_deltaTevp} = \texttt{SEAICIE\_deltaTdyn}/120$ ) within the physical ocean model time step (although this parameter is under debate), to allow for elastic waves to disappear. Because the scheme does not require a matrix inversion it is fast in spite of the small internal timestep and simple to implement on parallel computers [Hunke and Dukowicz, 1997]. For completeness, we repeat the equations for the components of the stress tensor $ \sigma_{1} = \sigma_{11}+\sigma_{22}$ , $ \sigma_{2}= \sigma_{11}-\sigma_{22}$ , and $ \sigma_{12}$ . Introducing the divergence $ D_D = \dot{\epsilon}_{11}+\dot{\epsilon}_{22}$ , and the horizontal tension and shearing strain rates, $ D_T = \dot{\epsilon}_{11}-\dot{\epsilon}_{22}$ and $ D_S = 2\dot{\epsilon}_{12}$ , respectively, and using the above abbreviations, the equations 6.49 can be written as:


Here, the elastic parameter $ E$ is redefined in terms of a damping timescale $ T$ for elastic waves

$\displaystyle E=\frac{\zeta}{T}.$

$ T=E_{0}\Delta{t}$ with the tunable parameter $ E_0<1$ and the external (long) timestep $ \Delta{t}$ . $ E_{0} = \frac{1}{3}$ is the default value in the code and close to what Hunke and Dukowicz [1997] and Hunke [2001] recommend.

To use the EVP solver, make sure that both SEAICE_CGRID and SEAICE_ALLOW_EVP are defined in SEAICE_OPTIONS.h (default). The solver is turned on by setting the sub-cycling time step SEAICE_deltaTevp to a value larger than zero. The choice of this time step is under debate. Hunke and Dukowicz [1997] recommend order(120) time steps for the EVP solver within one model time step $ \Delta{t}$ (deltaTmom). One can also choose order(120) time steps within the forcing time scale, but then we recommend adjusting the damping time scale $ T$ accordingly, by setting either SEAICE_elasticParm ($ E_{0}$ ), so that $ E_{0}\Delta{t}=$forcing time scale , or directly SEAICE_evpTauRelax ($ T$ ) to the forcing time scale.


6.6.2.4.7 More stable variants of Elastic-Viscous-Plastic Dynamics: EVP* , mEVP, and aEVP

 
The genuine EVP schemes appears to give noisy solutions [Bouillon et al., 2013; Lemieux et al., 2012; Hunke, 2001]. This has lead to a modified EVP or EVP* [Bouillon et al., 2013; Kimmritz et al., 2015; Lemieux et al., 2012]; here, we refer to these variants by modified EVP (mEVP) and adaptive EVP (aEVP) [Kimmritz et al., 2016]. The main idea is to modify the ``natural'' time-discretization of the momentum equations:

$\displaystyle m\frac{D\vec{u}}{Dt} \approx m\frac{u^{p+1}-u^{n}}{\Delta{t}} + \beta^{*}\frac{u^{p+1}-u^{p}}{\Delta{t}_{\mathrm{EVP}}}$ (6.53)

where $ n$ is the previous time step index, and $ p$ is the previous sub-cycling index. The extra ``intertial'' term $ m\,(u^{p+1}-u^{n})/\Delta{t})$ allows the definition of a residual $ \vert u^{p+1}-u^{p}\vert$ that, as $ u^{p+1} \rightarrow u^{n+1}$ , converges to 0 . In this way EVP can be re-interpreted as a pure iterative solver where the sub-cycling has no association with time-relation (through $ \Delta{t}_{\mathrm{EVP}}$ ) [Bouillon et al., 2013; Kimmritz et al., 2015]. Using the terminology of Kimmritz et al. [2015], the evolution equations of stress $ \sigma_{ij}$ and momentum $ \vec{u}$ can be written as:


$ \vec{R}$ contains all terms in the momentum equations except for the rheology terms and the time derivative; $ \alpha $ and $ \beta$ are free parameters (SEAICE_evpAlpha, SEAICE_evpBeta) that replace the time stepping parameters SEAICE_deltaTevp ( $ \Delta{T}_{\mathrm{EVP}}$ ), SEAICE_elasticParm ($ E_{0}$ ), or SEAICE_evpTauRelax ($ T$ ). $ \alpha $ and $ \beta$ determine the speed of convergence and the stability. Usually, it makes sense to use $ \alpha = \beta$ , and SEAICEnEVPstarSteps $ \gg (\alpha,\,\beta)$ [Kimmritz et al., 2015]. Currently, there is no termination criterion and the number of mEVP iterations is fixed to SEAICEnEVPstarSteps.

In order to use mEVP in the MITgcm, set SEAICEuseEVPstar = .TRUE., in data.seaice. If SEAICEuseEVPrev =.TRUE., the actual form of equations (6.54) and (6.55) is used with fewer implicit terms and the factor of $ e^{2}$ dropped in the stress equations (6.51) and (6.52). Although this modifies the original EVP-equations, it turns out to improve convergence [Bouillon et al., 2013].

Another variant is the aEVP scheme [Kimmritz et al., 2016], where the value of $ \alpha $ is set dynamically based on the stability criterion

$\displaystyle \alpha = \beta = \max\left( \tilde{c}\pi\sqrt{c \frac{\zeta}{A_{c}} \frac{\Delta{t}}{\max(m,10^{-4}\text{\,kg})}},\alpha_{\min} \right)$ (6.56)

with the grid cell area $ A_c$ and the ice and snow mass $ m$ . This choice sacrifices speed of convergence for stability with the result that aEVP converges quickly to VP where $ \alpha $ can be small and more slowly in areas where the equations are stiff. In practice, aEVP leads to an overall better convergence than mEVP [Kimmritz et al., 2016]. To use aEVP in the MITgcm set SEAICEaEVPcoeff $ = \tilde{c}$ ; this also sets the default values of SEAICEaEVPcStar ($ c=4$ ) and SEAICEaEVPalphaMin ( $ \alpha_{\min}=5$ ). Good convergence has been obtained with setting these values [Kimmritz et al., 2016]: SEAICEaEVPcoeff = 0.5, SEAICEnEVPstarSteps = 500, SEAICEuseEVPstar = .TRUE., SEAICEuseEVPrev = .TRUE.

Note, that probably because of the C-grid staggering of velocities and stresses, mEVP may not converge as successfully as in Kimmritz et al. [2015], and that convergence at very high resolution (order 5km) has not been studied yet.


6.6.2.4.8 Truncated ellipse method (TEM) for yield curve

 
In the so-called truncated ellipse method the shear viscosity $ \eta $ is capped to suppress any tensile stress [Geiger et al., 1998; Hibler and Schulson, 1997]:

$\displaystyle \eta = \min\left(\frac{\zeta}{e^2}, \frac{\frac{P}{2}-\zeta(\dot{... ...,(\dot{\epsilon}_{11}-\dot{\epsilon}_{22})^2 +4\dot{\epsilon}_{12}^2})}\right).$ (6.57)

To enable this method, set #define SEAICE_ALLOW_TEM in SEAICE_OPTIONS.h and turn it on with SEAICEuseTEM in data.seaice.


6.6.2.4.9 Ice-Ocean stress

 
Moving sea ice exerts a stress on the ocean which is the opposite of the stress $ \ensuremath{\vec{\mathbf{\mathbf{\tau}}}}_{ocean}$ in Eq. 6.39. This stess is applied directly to the surface layer of the ocean model. An alternative ocean stress formulation is given by Hibler and Bryan [1987]. Rather than applying $ \ensuremath{\vec{\mathbf{\mathbf{\tau}}}}_{ocean}$ directly, the stress is derived from integrating over the ice thickness to the bottom of the oceanic surface layer. In the resulting equation for the combined ocean-ice momentum, the interfacial stress cancels and the total stress appears as the sum of windstress and divergence of internal ice stresses: $ \delta(z) (\ensuremath{\vec{\mathbf{\mathbf{\tau}}}}_{air} + \ensuremath{\vec{\mathbf{F}}})/\rho_0$ , [see also Eq.2 of Hibler and Bryan, 1987]. The disadvantage of this formulation is that now the velocity in the surface layer of the ocean that is used to advect tracers, is really an average over the ocean surface velocity and the ice velocity leading to an inconsistency as the ice temperature and salinity are different from the oceanic variables. To turn on the stress formulation of Hibler and Bryan [1987], set useHB87StressCoupling=.TRUE. in data.seaice.


6.6.2.4.10 Finite-volume discretization of the stress tensor divergence

 
On an Arakawa C grid, ice thickness and concentration and thus ice strength $ P$ and bulk and shear viscosities $ \zeta$ and $ \eta $ are naturally defined a C-points in the center of the grid cell. Discretization requires only averaging of $ \zeta$ and $ \eta $ to vorticity or Z-points (or $ \zeta$ -points, but here we use Z in order avoid confusion with the bulk viscosity) at the bottom left corner of the cell to give $ \overline{\zeta}^{Z}$ and $ \overline{\eta}^{Z}$ . In the following, the superscripts indicate location at Z or C points, distance across the cell (F), along the cell edge (G), between $ u$ -points (U), $ v$ -points (V), and C-points (C). The control volumes of the $ u$ - and $ v$ -equations in the grid cell at indices $ (i,j)$ are $ A_{i,j}^{w}$ and $ A_{i,j}^{s}$ , respectively. With these definitions (which follow the model code documentation except that $ \zeta$ -points have been renamed to Z-points), the strain rates are discretized as:

$\displaystyle \dot{\epsilon}_{11}$ $\displaystyle = \partial_{1}{u}_{1} + k_{2}u_{2}$ (6.58)
$\displaystyle => (\epsilon_{11})_{i,j}^C$ $\displaystyle = \frac{u_{i+1,j}-u_{i,j}}{\Delta{x}_{i,j}^{F}} + k_{2,i,j}^{C}\frac{v_{i,j+1}+v_{i,j}}{2}$    
$\displaystyle \dot{\epsilon}_{22}$ $\displaystyle = \partial_{2}{u}_{2} + k_{1}u_{1}$ (6.59)
$\displaystyle => (\epsilon_{22})_{i,j}^C$ $\displaystyle = \frac{v_{i,j+1}-v_{i,j}}{\Delta{y}_{i,j}^{F}} + k_{1,i,j}^{C}\frac{u_{i+1,j}+u_{i,j}}{2}$    
$\displaystyle \dot{\epsilon}_{12} = \dot{\epsilon}_{21}$ $\displaystyle = \frac{1}{2}\biggl( \partial_{1}{u}_{2} + \partial_{2}{u}_{1} - k_{1}u_{2} - k_{2}u_{1} \biggr)$ (6.60)
$\displaystyle => (\epsilon_{12})_{i,j}^Z$ $\displaystyle = \frac{1}{2} \biggl( \frac{v_{i,j}-v_{i-1,j}}{\Delta{x}_{i,j}^V} + \frac{u_{i,j}-u_{i,j-1}}{\Delta{y}_{i,j}^U}$    
  $\displaystyle \phantom{=\frac{1}{2}\biggl(} - k_{1,i,j}^{Z}\frac{v_{i,j}+v_{i-1,j}}{2} - k_{2,i,j}^{Z}\frac{u_{i,j}+u_{i,j-1}}{2} \biggr),$    

so that the diagonal terms of the strain rate tensor are naturally defined at C-points and the symmetric off-diagonal term at Z-points. No-slip boundary conditions ( $ u_{i,j-1}+u_{i,j}=0$ and $ v_{i-1,j}+v_{i,j}=0$ across boundaries) are implemented via ``ghost-points''; for free slip boundary conditions $ (\epsilon_{12})^Z=0$ on boundaries.

For a spherical polar grid, the coefficients of the metric terms are $ k_{1}=0$ and $ k_{2}=-\tan\phi/a$ , with the spherical radius $ a$ and the latitude $ \phi $ ; $ \Delta{x}_1 = \Delta{x} = a\cos\phi \Delta\lambda$ , and $ \Delta{x}_2 = \Delta{y}=a\Delta\phi$ . For a general orthogonal curvilinear grid, $ k_{1}$ and $ k_{2}$ can be approximated by finite differences of the cell widths:

$\displaystyle k_{1,i,j}^{C}$ $\displaystyle = \frac{1}{\Delta{y}_{i,j}^{F}} \frac{\Delta{y}_{i+1,j}^{G}-\Delta{y}_{i,j}^{G}}{\Delta{x}_{i,j}^{F}}$ (6.61)
$\displaystyle k_{2,i,j}^{C}$ $\displaystyle = \frac{1}{\Delta{x}_{i,j}^{F}} \frac{\Delta{x}_{i,j+1}^{G}-\Delta{x}_{i,j}^{G}}{\Delta{y}_{i,j}^{F}}$ (6.62)
$\displaystyle k_{1,i,j}^{Z}$ $\displaystyle = \frac{1}{\Delta{y}_{i,j}^{U}} \frac{\Delta{y}_{i,j}^{C}-\Delta{y}_{i-1,j}^{C}}{\Delta{x}_{i,j}^{V}}$ (6.63)
$\displaystyle k_{2,i,j}^{Z}$ $\displaystyle = \frac{1}{\Delta{x}_{i,j}^{V}} \frac{\Delta{x}_{i,j}^{C}-\Delta{x}_{i,j-1}^{C}}{\Delta{y}_{i,j}^{U}}$ (6.64)

The stress tensor is given by the constitutive viscous-plastic relation $ \sigma_{\alpha\beta} = 2\eta\dot{\epsilon}_{\alpha\beta} + [(\zeta-\eta)\dot{\epsilon}_{\gamma\gamma} - P/2 ]\delta_{\alpha\beta}$ [Hibler, 1979]. The stress tensor divergence $ (\nabla\sigma)_{\alpha} = \partial_\beta\sigma_{\beta\alpha}$ , is discretized in finite volumes [see also Losch et al., 2010]. This conveniently avoids dealing with further metric terms, as these are ``hidden'' in the differential cell widths. For the $ u$ -equation ($ \alpha=1$ ) we have:

$\displaystyle (\nabla\sigma)_{1}: \phantom{=}$ $\displaystyle \frac{1}{A_{i,j}^w} \int_{\mathrm{cell}}(\partial_1\sigma_{11}+\partial_2\sigma_{21})\,dx_1\,dx_2$ (6.65)
$\displaystyle =$ $\displaystyle \frac{1}{A_{i,j}^w} \biggl\{ \int_{x_2}^{x_2+\Delta{x}_2}\sigma_{... ...+\Delta{x}_1}\sigma_{21}dx_1\biggl\vert _{x_{2}}^{x_{2}+\Delta{x}_{2}} \biggr\}$    
$\displaystyle \approx$ $\displaystyle \frac{1}{A_{i,j}^w} \biggl\{ \Delta{x}_2\sigma_{11}\biggl\vert _{... ...1}} + \Delta{x}_1\sigma_{21}\biggl\vert _{x_{2}}^{x_{2}+\Delta{x}_{2}} \biggr\}$    
$\displaystyle =$ $\displaystyle \frac{1}{A_{i,j}^w} \biggl\{ (\Delta{x}_2\sigma_{11})_{i,j}^C - (\Delta{x}_2\sigma_{11})_{i-1,j}^C$    
$\displaystyle \phantom{\frac{1}{A_{i,j}^w} \biggl\{} + (\Delta{x}_1\sigma_{21})_{i,j+1}^Z - (\Delta{x}_1\sigma_{21})_{i,j}^Z \biggr\}$    

with

$\displaystyle (\Delta{x}_2\sigma_{11})_{i,j}^C =$ $\displaystyle \phantom{+} \Delta{y}_{i,j}^{F}(\zeta + \eta)^{C}_{i,j} \frac{u_{i+1,j}-u_{i,j}}{\Delta{x}_{i,j}^{F}}$ (6.66)
  $\displaystyle + \Delta{y}_{i,j}^{F}(\zeta + \eta)^{C}_{i,j} k_{2,i,j}^C \frac{v_{i,j+1}+v_{i,j}}{2}$    
$\displaystyle + \Delta{y}_{i,j}^{F}(\zeta - \eta)^{C}_{i,j} \frac{v_{i,j+1}-v_{i,j}}{\Delta{y}_{i,j}^{F}}$    
$\displaystyle + \Delta{y}_{i,j}^{F}(\zeta - \eta)^{C}_{i,j} k_{1,i,j}^{C}\frac{u_{i+1,j}+u_{i,j}}{2}$    
$\displaystyle - \Delta{y}_{i,j}^{F} \frac{P}{2}$    
$\displaystyle (\Delta{x}_1\sigma_{21})_{i,j}^Z =$ $\displaystyle \phantom{+} \Delta{x}_{i,j}^{V}\overline{\eta}^{Z}_{i,j} \frac{u_{i,j}-u_{i,j-1}}{\Delta{y}_{i,j}^{U}}$ (6.67)
  $\displaystyle + \Delta{x}_{i,j}^{V}\overline{\eta}^{Z}_{i,j} \frac{v_{i,j}-v_{i-1,j}}{\Delta{x}_{i,j}^{V}}$    
  $\displaystyle - \Delta{x}_{i,j}^{V}\overline{\eta}^{Z}_{i,j} k_{2,i,j}^{Z}\frac{u_{i,j}+u_{i,j-1}}{2}$    
  $\displaystyle - \Delta{x}_{i,j}^{V}\overline{\eta}^{Z}_{i,j} k_{1,i,j}^{Z}\frac{v_{i,j}+v_{i-1,j}}{2}$    

Similarly, we have for the $ v$ -equation ($ \alpha=2$ ):

$\displaystyle (\nabla\sigma)_{2}: \phantom{=}$ $\displaystyle \frac{1}{A_{i,j}^s} \int_{\mathrm{cell}}(\partial_1\sigma_{12}+\partial_2\sigma_{22})\,dx_1\,dx_2$ (6.68)
$\displaystyle =$ $\displaystyle \frac{1}{A_{i,j}^s} \biggl\{ \int_{x_2}^{x_2+\Delta{x}_2}\sigma_{... ...+\Delta{x}_1}\sigma_{22}dx_1\biggl\vert _{x_{2}}^{x_{2}+\Delta{x}_{2}} \biggr\}$    
$\displaystyle \approx$ $\displaystyle \frac{1}{A_{i,j}^s} \biggl\{ \Delta{x}_2\sigma_{12}\biggl\vert _{... ...1}} + \Delta{x}_1\sigma_{22}\biggl\vert _{x_{2}}^{x_{2}+\Delta{x}_{2}} \biggr\}$    
$\displaystyle =$ $\displaystyle \frac{1}{A_{i,j}^s} \biggl\{ (\Delta{x}_2\sigma_{12})_{i+1,j}^Z - (\Delta{x}_2\sigma_{12})_{i,j}^Z$    
$\displaystyle \phantom{\frac{1}{A_{i,j}^s} \biggl\{} + (\Delta{x}_1\sigma_{22})_{i,j}^C - (\Delta{x}_1\sigma_{22})_{i,j-1}^C \biggr\}$    

with

$\displaystyle (\Delta{x}_1\sigma_{12})_{i,j}^Z =$ $\displaystyle \phantom{+} \Delta{y}_{i,j}^{U}\overline{\eta}^{Z}_{i,j} \frac{u_{i,j}-u_{i,j-1}}{\Delta{y}_{i,j}^{U}}$ (6.69)
  $\displaystyle + \Delta{y}_{i,j}^{U}\overline{\eta}^{Z}_{i,j} \frac{v_{i,j}-v_{i-1,j}}{\Delta{x}_{i,j}^{V}}$    
  $\displaystyle - \Delta{y}_{i,j}^{U}\overline{\eta}^{Z}_{i,j} k_{2,i,j}^{Z}\frac{u_{i,j}+u_{i,j-1}}{2}$    
  $\displaystyle - \Delta{y}_{i,j}^{U}\overline{\eta}^{Z}_{i,j} k_{1,i,j}^{Z}\frac{v_{i,j}+v_{i-1,j}}{2}$    
$\displaystyle (\Delta{x}_2\sigma_{22})_{i,j}^C =$ $\displaystyle \phantom{+} \Delta{x}_{i,j}^{F}(\zeta - \eta)^{C}_{i,j} \frac{u_{i+1,j}-u_{i,j}}{\Delta{x}_{i,j}^{F}}$    
  $\displaystyle + \Delta{x}_{i,j}^{F}(\zeta - \eta)^{C}_{i,j} k_{2,i,j}^{C} \frac{v_{i,j+1}+v_{i,j}}{2}$    
  $\displaystyle + \Delta{x}_{i,j}^{F}(\zeta + \eta)^{C}_{i,j} \frac{v_{i,j+1}-v_{i,j}}{\Delta{y}_{i,j}^{F}}$    
  $\displaystyle + \Delta{x}_{i,j}^{F}(\zeta + \eta)^{C}_{i,j} k_{1,i,j}^{C}\frac{u_{i+1,j}+u_{i,j}}{2}$    
  $\displaystyle -\Delta{x}_{i,j}^{F} \frac{P}{2}$    

Again, no slip boundary conditions are realized via ghost points and $ u_{i,j-1}+u_{i,j}=0$ and $ v_{i-1,j}+v_{i,j}=0$ across boundaries. For free slip boundary conditions the lateral stress is set to zeros. In analogy to $ (\epsilon_{12})^Z=0$ on boundaries, we set $ \sigma_{21}^{Z}=0$ , or equivalently $ \eta_{i,j}^{Z}=0$ , on boundaries.


6.6.2.4.11 Thermodynamics

 
NOTE: THIS SECTION IS TERRIBLY OUT OF DATE
In its original formulation the sea ice model [Menemenlis et al., 2005] uses simple thermodynamics following the appendix of Semtner [1976]. This formulation does not allow storage of heat, that is, the heat capacity of ice is zero. Upward conductive heat flux is parameterized assuming a linear temperature profile and together with a constant ice conductivity. It is expressed as $ (K/h)(T_{w}-T_{0})$ , where $ K$ is the ice conductivity, $ h$ the ice thickness, and $ T_{w}-T_{0}$ the difference between water and ice surface temperatures. This type of model is often refered to as a ``zero-layer'' model. The surface heat flux is computed in a similar way to that of Parkinson and Washington [1979] and Manabe et al. [1979].

The conductive heat flux depends strongly on the ice thickness $ h$ . However, the ice thickness in the model represents a mean over a potentially very heterogeneous thickness distribution. In order to parameterize a sub-grid scale distribution for heat flux computations, the mean ice thickness $ h$ is split into $ N $ thickness categories $ H_{n}$ that are equally distributed between $ 2h$ and a minimum imposed ice thickness of $ 5$ cm by $ H_n= \frac{2n-1}{7}\,h$ for $ n\in[1,N]$ . The heat fluxes computed for each thickness category is area-averaged to give the total heat flux [Hibler, 1984]. To use this thickness category parameterization set SEAICE_multDim to the number of desired categories (7 is a good guess, for anything larger than 7 modify SEAICE_SIZE.h) in data.seaice; note that this requires different restart files and switching this flag on in the middle of an integration is not advised. In order to include the same distribution for snow, set SEAICE_useMultDimSnow = .TRUE.; only then, the parameterization of always having a fraction of thin ice is efficient and generally thicker ice is produced [Castro-Morales et al., 2014].

The atmospheric heat flux is balanced by an oceanic heat flux from below. The oceanic flux is proportional to $ \rho\,c_{p}\left(T_{w}-T_{fr}\right)$ where $ \rho $ and $ c_{p}$ are the density and heat capacity of sea water and $ T_{fr}$ is the local freezing point temperature that is a function of salinity. This flux is not assumed to instantaneously melt or create ice, but a time scale of three days (run-time parameter SEAICE_gamma_t) is used to relax $ T_{w}$ to the freezing point. The parameterization of lateral and vertical growth of sea ice follows that of Hibler [1980,1979]; the so-called lead closing parameter $ h_{0}$ (run-time parameter HO) has a default value of 0.5 meters.

On top of the ice there is a layer of snow that modifies the heat flux and the albedo [Zhang et al., 1998]. Snow modifies the effective conductivity according to

$\displaystyle \frac{K}{h} \rightarrow \frac{1}{\frac{h_{s}}{K_{s}}+\frac{h}{K}},$

where $ K_s$ is the conductivity of snow and $ h_s$ the snow thickness. If enough snow accumulates so that its weight submerges the ice and the snow is flooded, a simple mass conserving parameterization of snowice formation (a flood-freeze algorithm following Archimedes' principle) turns snow into ice until the ice surface is back at $ z=0$ [Leppäranta, 1983]. The flood-freeze algorithm is enabled with the CPP-flag SEAICE_ALLOW_FLOODING and turned on with run-time parameter SEAICEuseFlooding=.true..


6.6.2.4.12 Advection of thermodynamic variables

 
Effective ice thickness (ice volume per unit area, $ c\cdot{h}$ ), concentration $ c$ and effective snow thickness ( $ c\cdot{h}_{s}$ ) are advected by ice velocities:

$\displaystyle \frac{\partial{X}}{\partial{t}} = - \nabla\cdot\left(\ensuremath{\vec{\mathbf{u}}}\,X\right) + \Gamma_{X} + D_{X}$ (6.70)

where $ \Gamma_X$ are the thermodynamic source terms and $ D_{X}$ the diffusive terms for quantities $ X=(c\cdot{h}), c, (c\cdot{h}_{s})$ . From the various advection scheme that are available in the MITgcm, we recommend flux-limited schemes [multidimensional 2nd and 3rd-order advection scheme with flux limiter Hundsdorfer and Trompert, 1994; Roe, 1985] to preserve sharp gradients and edges that are typical of sea ice distributions and to rule out unphysical over- and undershoots (negative thickness or concentration). These schemes conserve volume and horizontal area and are unconditionally stable, so that we can set $ D_{X}=0$ . Run-timeflags: SEAICEadvScheme (default=2, is the historic 2nd-order, centered difference scheme), DIFF1 = $ D_{X}/\Delta{x}$ (default=0.004).

The MITgcm sea ice model provides the option to use the thermodynamics model of Winton [2000], which in turn is based on the 3-layer model of Semtner [1976] and which treats brine content by means of enthalpy conservation; the corresponding package thsice is described in section 6.6.1. This scheme requires additional state variables, namely the enthalpy of the two ice layers (instead of effective ice salinity), to be advected by ice velocities. The internal sea ice temperature is inferred from ice enthalpy. To avoid unphysical (negative) values for ice thickness and concentration, a positive 2nd-order advection scheme with a SuperBee flux limiter [Roe, 1985] should be used to advect all sea-ice-related quantities of the Winton [2000] thermodynamic model (runtime flag thSIceAdvScheme=77 and thSIce_diffK=$ D_{X}$ =0 in data.ice, defaults are 0). Because of the non-linearity of the advection scheme, care must be taken in advecting these quantities: when simply using ice velocity to advect enthalpy, the total energy (i.e., the volume integral of enthalpy) is not conserved. Alternatively, one can advect the energy content (i.e., product of ice-volume and enthalpy) but then false enthalpy extrema can occur, which then leads to unrealistic ice temperature. In the currently implemented solution, the sea-ice mass flux is used to advect the enthalpy in order to ensure conservation of enthalpy and to prevent false enthalpy extrema.


6.6.2.5 Key subroutines

Top-level routine: seaice_model.F 

C     !CALLING SEQUENCE:
c ...
c  seaice_model (TOP LEVEL ROUTINE)
c  |
c  |-- #ifdef SEAICE_CGRID
c  |     SEAICE_DYNSOLVER
c  |     |
c  |     |-- < compute proxy for geostrophic velocity >
c  |     |
c  |     |-- < set up mass per unit area and Coriolis terms >
c  |     |
c  |     |-- < dynamic masking of areas with no ice >
c  |     |
c  |     |

c  |   #ELSE
c  |     DYNSOLVER
c  |   #ENDIF
c  |
c  |-- if ( useOBCS ) 
c  |     OBCS_APPLY_UVICE
c  |
c  |-- if ( SEAICEadvHeff .OR. SEAICEadvArea .OR. SEAICEadvSnow .OR. SEAICEadvSalt )
c  |     SEAICE_ADVDIFF
c  |
c  |-- if ( usePW79thermodynamics ) 
c  |     SEAICE_GROWTH
c  |
c  |-- if ( useOBCS ) 
c  |     if ( SEAICEadvHeff ) OBCS_APPLY_HEFF
c  |     if ( SEAICEadvArea ) OBCS_APPLY_AREA
c  |     if ( SEAICEadvSALT ) OBCS_APPLY_HSALT
c  |     if ( SEAICEadvSNOW ) OBCS_APPLY_HSNOW
c  |
c  |-- < do various exchanges >
c  |
c  |-- < do additional diagnostics >
c  |
c  o


6.6.2.6 SEAICE diagnostics

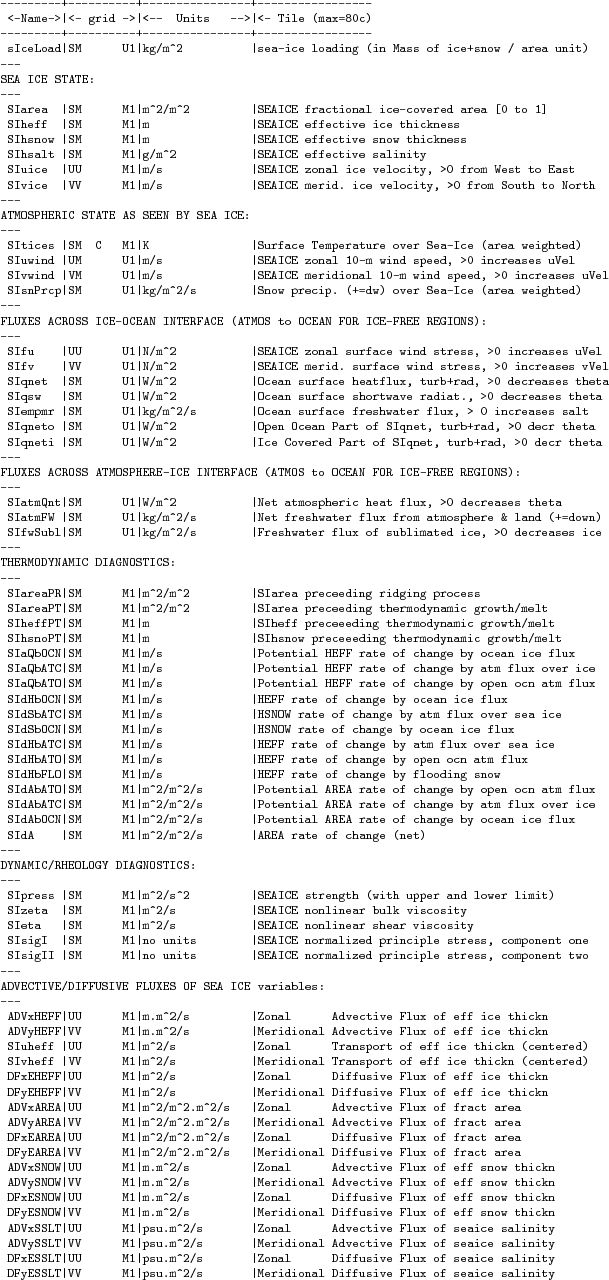
Diagnostics output is available via the diagnostics package (see Section 7.1). Available output fields are summarized in Table 6.6.2.6.


Table 6.20: Available diagnostics of the seaice-package
\begin{table}\centering {\footnotesize \begin{verbatim}---------+----------+--... ... \vert Meridional Diffusive Flux of seaice salinity\end{verbatim} }\end{table}



6.6.2.7 Experiments and tutorials that use seaice

  • Labrador Sea experiment in lab_sea verification directory.
  • seaice_obcs, based on lab_sea
  • offline_exf_seaice/input.seaicetd, based on lab_sea
  • global_ocean.cs32x15/input.icedyn and global_ocean.cs32x15/input.seaice, global cubed-sphere-experiment with combinations of seaice and thsice

next up previous contents
Next: 6.6.3 SHELFICE Package Up: 6.6 Sea Ice Packages Previous: 6.6.1 THSICE: The Thermodynamic   Contents
mitgcm-support@mitgcm.org
Copyright © 2006 Massachusetts Institute of Technology Last update 2018-01-23