|
|
|
|



Next: 3.10.2 Discrete Numerical Configuration
Up: 3.10 Global Ocean MITgcm
Previous: 3.10 Global Ocean MITgcm
Contents
3.10.1 Overview
The model is forced with climatological wind stress data and surface
flux data from DaSilva [10]. Climatological data
from Levitus [36] is used to initialize the model hydrography.
Levitus seasonal climatology data is also used throughout the calculation
to provide additional air-sea fluxes.
These fluxes are combined with the DaSilva climatological estimates of
surface heat flux and fresh water, resulting in a mixed boundary
condition of the style described in Haney [25].
Altogether, this yields the following forcing applied
in the model surface layer.
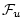 |
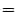 |
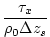 |
(3.30) |
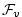 |
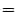 |
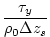 |
(3.31) |
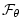 |
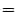 |
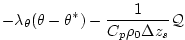 |
(3.32) |
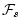 |
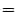 |
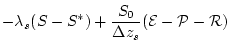 |
(3.33) |
where
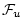 , ,
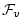 , ,
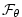 , ,
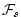 are the forcing terms in the zonal and meridional
momentum and in the potential temperature and salinity
equations respectively.
The term are the forcing terms in the zonal and meridional
momentum and in the potential temperature and salinity
equations respectively.
The term
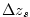 represents the top ocean layer thickness in
meters.
It is used in conjunction with a reference density, represents the top ocean layer thickness in
meters.
It is used in conjunction with a reference density, 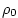 (here set to
(here set to
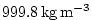 ), a
reference salinity, ), a
reference salinity, 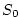 (here set to 35 ppt),
and a specific heat capacity, (here set to 35 ppt),
and a specific heat capacity, 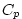 (here set to (here set to
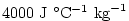 ), to convert
input dataset values into time tendencies of
potential temperature (with units of ), to convert
input dataset values into time tendencies of
potential temperature (with units of
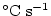 ),
salinity (with units ),
salinity (with units
 ) and
velocity (with units ) and
velocity (with units
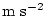 ).
The externally supplied forcing fields used in this
experiment are ).
The externally supplied forcing fields used in this
experiment are 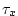 , , 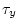 , ,
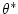 , , 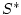 , ,
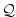 and and
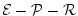 . The wind stress fields ( . The wind stress fields (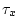 , , 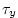 )
have units of )
have units of
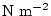 . The temperature forcing fields
( . The temperature forcing fields
(
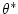 and and 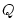 ) have units of ) have units of
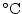 and and
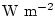 respectively. The salinity forcing fields (
respectively. The salinity forcing fields (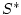 and and
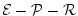 ) have units of ) have units of 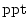 and and
 respectively. The source files and procedures for ingesting this data into the
simulation are described in the experiment configuration discussion in section
3.10.3.
respectively. The source files and procedures for ingesting this data into the
simulation are described in the experiment configuration discussion in section
3.10.3.



Next: 3.10.2 Discrete Numerical Configuration
Up: 3.10 Global Ocean MITgcm
Previous: 3.10 Global Ocean MITgcm
Contents
mitgcm-support@dev.mitgcm.org
| Copyright © 2002
Massachusetts Institute of Technology |
 |
|







