|
|
|
|



Next: 5.3.2 Code configuration
Up: 5.3 Sensitivity of Air-Sea
Previous: 5.3 Sensitivity of Air-Sea
Contents
Subsections
5.3.1 Overview of the experiment
We describe an adjoint sensitivity analysis of out-gassing from
the ocean into the atmosphere of a carbon-like tracer injected
into the ocean interior (see [29]).
5.3.1.1 Passive tracer equation
For this work the MITGCM was augmented with a thermodynamically
inactive tracer, 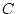 . Tracer residing in the ocean
model surface layer is out-gassed according to a relaxation time scale, . Tracer residing in the ocean
model surface layer is out-gassed according to a relaxation time scale,
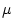 . Within the ocean interior, the tracer is passively advected
by the ocean model currents. The full equation for the time evolution . Within the ocean interior, the tracer is passively advected
by the ocean model currents. The full equation for the time evolution
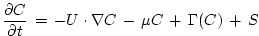 |
(5.15) |
also includes a source term 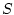 . This term
represents interior sources of . This term
represents interior sources of 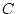 such as would arise due to
direct injection.
The velocity term, such as would arise due to
direct injection.
The velocity term, 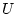 , is the sum of the
model Eulerian circulation and an eddy-induced velocity, the latter
parameterized according to Gent/McWilliams
([16,17]).
The convection function, , is the sum of the
model Eulerian circulation and an eddy-induced velocity, the latter
parameterized according to Gent/McWilliams
([16,17]).
The convection function, 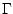 , mixes , mixes 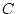 vertically wherever the
fluid is locally statically unstable. vertically wherever the
fluid is locally statically unstable.
The out-gassing time scale, 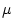 , in eqn. (5.15)
is set so that , in eqn. (5.15)
is set so that
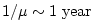 for the surface
ocean and for the surface
ocean and 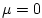 elsewhere. With this value, eqn. (5.15)
is valid as a prognostic equation for small perturbations in oceanic
carbon concentrations. This configuration provides a
powerful tool for examining the impact of large-scale ocean circulation
on elsewhere. With this value, eqn. (5.15)
is valid as a prognostic equation for small perturbations in oceanic
carbon concentrations. This configuration provides a
powerful tool for examining the impact of large-scale ocean circulation
on 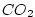 out-gassing due to interior injections.
As source we choose a constant in time injection of out-gassing due to interior injections.
As source we choose a constant in time injection of
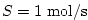 . .
5.3.1.2 Model configuration
The model configuration employed has a constant
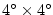 resolution horizontal grid and realistic
geography and bathymetry. Twenty vertical layers are used with
vertical spacing ranging
from 50 m near the surface to 815 m at depth.
Driven to steady-state by climatological wind-stress, heat and
fresh-water forcing the model reproduces well known large-scale
features of the ocean general circulation. resolution horizontal grid and realistic
geography and bathymetry. Twenty vertical layers are used with
vertical spacing ranging
from 50 m near the surface to 815 m at depth.
Driven to steady-state by climatological wind-stress, heat and
fresh-water forcing the model reproduces well known large-scale
features of the ocean general circulation.
5.3.1.3 Out-gassing cost function
To quantify and understand out-gassing due to injections of 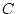 in eqn. (5.15),
we define a cost function
in eqn. (5.15),
we define a cost function 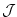 that measures the total amount of
tracer out-gassed at each timestep: that measures the total amount of
tracer out-gassed at each timestep:
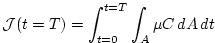 |
(5.16) |
Equation(5.16) integrates the out-gassing term, 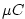 ,
from (5.15)
over the entire ocean surface area, ,
from (5.15)
over the entire ocean surface area, 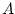 , and accumulates it
up to time , and accumulates it
up to time 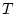 .
Physically, .
Physically, 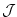 can be thought of as representing the amount of can be thought of as representing the amount of
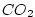 that our model predicts would be out-gassed following an
injection at rate that our model predicts would be out-gassed following an
injection at rate 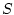 .
The sensitivity of .
The sensitivity of 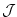 to the spatial location of to the spatial location of 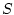 , ,
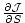 ,
can be used to identify regions from which circulation
would cause ,
can be used to identify regions from which circulation
would cause 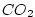 to rapidly out-gas following injection
and regions in which to rapidly out-gas following injection
and regions in which 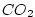 injections would remain effectively
sequestered within the ocean. injections would remain effectively
sequestered within the ocean.



Next: 5.3.2 Code configuration
Up: 5.3 Sensitivity of Air-Sea
Previous: 5.3 Sensitivity of Air-Sea
Contents
mitgcm-support@dev.mitgcm.org
| Copyright © 2002
Massachusetts Institute of Technology |
 |
|







