 |
 |
|||||||||||
 |
|
|||||||||||
 |
 |
|||||||||||
|
Next: 1.3.5 Solution strategy Up: 1.3 Continuous equations in Previous: 1.3.3 Ocean Contents Subsections
|
making a small correction to the hydrostatic pressure.
QH has good energetic credentials - they are the same as for HPE. Importantly, however, it has the same angular momentum principle as the full non-hydrostatic model (NH) - see Marshall et.al., 1997a. As in HPE only a 2-d elliptic problem need be solved.
1.3.4.3 Non-hydrostatic and quasi-nonhydrostatic forms
MITgcm presently supports a full non-hydrostatic ocean isomorph, but only a quasi-non-hydrostatic atmospheric isomorph.
1.3.4.3.1 Non-hydrostatic Ocean
In the non-hydrostatic ocean model all terms in equations Eqs.(1.29
![]() 1.31) are retained. A
three dimensional elliptic equation must be solved subject to Neumann
boundary conditions (see below). It is important to note that use of the
full NH does not admit any new `fast' waves in to the system - the
incompressible condition eq(1.3) has already filtered out
acoustic modes. It does, however, ensure that the gravity waves are treated
accurately with an exact dispersion relation. The NH set has a
complete angular momentum principle and consistent energetics - see White
and Bromley, 1995; Marshall et.al. 1997a.
1.31) are retained. A
three dimensional elliptic equation must be solved subject to Neumann
boundary conditions (see below). It is important to note that use of the
full NH does not admit any new `fast' waves in to the system - the
incompressible condition eq(1.3) has already filtered out
acoustic modes. It does, however, ensure that the gravity waves are treated
accurately with an exact dispersion relation. The NH set has a
complete angular momentum principle and consistent energetics - see White
and Bromley, 1995; Marshall et.al. 1997a.
1.3.4.3.2 Quasi-nonhydrostatic Atmosphere
In the non-hydrostatic version of our atmospheric model we approximate ![]() in the vertical momentum eqs(1.28) and (1.30)
(but only here) by:
in the vertical momentum eqs(1.28) and (1.30)
(but only here) by:
where
1.3.4.4 Summary of equation sets supported by model
1.3.4.4.1 Atmosphere
Hydrostatic, and quasi-hydrostatic and quasi non-hydrostatic forms of the
compressible non-Boussinesq equations in ![]() coordinates are supported.
coordinates are supported.
1.3.4.4.1.1 Hydrostatic and quasi-hydrostatic
The hydrostatic set is written out in ![]() coordinates in appendix Atmosphere
- see eq(1.59).
coordinates in appendix Atmosphere
- see eq(1.59).
1.3.4.4.1.2 Quasi-nonhydrostatic
A quasi-nonhydrostatic form is also supported.
1.3.4.4.2 Ocean
1.3.4.4.2.1 Hydrostatic and quasi-hydrostatic
Hydrostatic, and quasi-hydrostatic forms of the incompressible Boussinesq
equations in ![]() coordinates are supported.
coordinates are supported.
1.3.4.4.2.2 Non-hydrostatic
Non-hydrostatic forms of the incompressible Boussinesq equations in ![]() coordinates are supported - see eqs(1.99) to (1.104).
coordinates are supported - see eqs(1.99) to (1.104).
Next: 1.3.5 Solution strategy Up: 1.3 Continuous equations in Previous: 1.3.3 Ocean Contents mitgcm-support@mitgcm.org



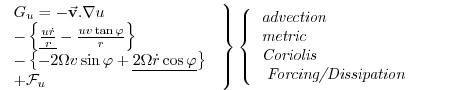


![\resizebox{5in}{!}{
\includegraphics*[0.5in,0.5in][7.5in,10.5in]{s_overview/figs/sphere.ps}
}](img203.png)


