6.2.4 exch2: Extended Cubed Sphere Topology

The exch2 package extends the original cubed sphere topology configuration to allow more flexible domain decomposition and parallelization. Cube faces (also called subdomains) may be divided into any number of tiles that divide evenly into the grid point dimensions of the subdomain. Furthermore, the tiles can run on separate processors individually or in groups, which provides for manual compile-time load balancing across a relatively arbitrary number of processors.

The exchange parameters are declared in pkg/exch2/W2_EXCH2_TOPOLOGY.h and assigned in pkg/exch2/w2_e2setup.F. The validity of the cube topology depends on the SIZE.h file as detailed below. The default files provided in the release configure a cubed sphere topology of six tiles, one per subdomain, each with 32 $\times$ 32 grid points, with all tiles running on a single processor. Both files are generated by Matlab scripts in utils/exch2/matlab-topology-generator; see Section 6.2.4.3 Generating Topology Files for exch2 for details on creating alternate topologies. Pregenerated examples of these files with alternate topologies are provided under utils/exch2/code-mods along with the appropriate SIZE.h file for single-processor execution.

6.2.4.2 Invoking exch2

At the time of this writing the following examples use exch2 and may be used for guidance:

6.2.4.3 Generating Topology Files for exch2

Alternate cubed sphere topologies may be created using the Matlab scripts in utils/exch2/matlab-topology-generator. Running the m-file driver.m from the Matlab prompt (there are no parameters to pass) generates exch2 topology files W2_EXCH2_TOPOLOGY.h and w2_e2setup.F in the working directory and displays a figure of the topology via Matlab - figures 6.4, 6.3, and 6.2 are examples of the generated diagrams. The other m-files in the directory are subroutines called from driver.m and should not be run ``bare'' except for development purposes.

The parameters that determine the dimensions and topology of the generated configuration are nr, nb, ng, tnx and tny, and all are assigned early in the script.

The first three determine the height and width of the subdomains and hence the size of the overall domain. Each one determines the number of grid points, and therefore the resolution, along the subdomain sides in a ``great circle'' around each the three spatial axes of the cube. At the time of this writing MITgcm requires these three parameters to be equal, but they provide for future releases to accomodate different resolutions around the axes to allow subdomains with differing resolutions.

The parameters tnx and tny determine the width and height of the tiles into which the subdomains are decomposed, and must evenly divide the integer assigned to nr, nb and ng. The result is a rectangular tiling of the subdomain. Figure 6.2 shows one possible topology for a twenty-four-tile cube, and figure 6.4 shows one for six tiles.

**Figure 6.2:** Plot of a cubed sphere topology with a 32 $\times$ 192 domain divided into six 32 $\times$ 32 subdomains, each of which is divided into eight tiles of width `tnx=16` and height `tny=8` for a total of forty-eight tiles. The colored borders of the subdomains represent the parameters `nr` (red), `ng` (green), and `nb` (blue). This tiling is used in the example verification/adjustment.cs-32x32x1/ with the option (blanklist.txt) to remove the land-only 4 tiles (11,12,13,14) which are filled in red on the plot.
$\resizebox{6in}{!}{ \includegraphics{s_phys_pkgs/figs/adjust_cs.ps} }$

**Figure 6.3:** Plot of a non-square cubed sphere topology with 6 subdomains of different size (nr=90,ng=360,nb=90), divided into one to four tiles each (`tnx=90, tny=90`), resulting in a total of 18 tiles.
$\resizebox{6in}{!}{ \includegraphics{s_phys_pkgs/figs/polarcap.ps} }$

**Figure 6.4:** Plot of a cubed sphere topology with a 32 $\times$ 192 domain divided into six 32 $\times$ 32 subdomains with one tile each (`tnx=32, tny=32`). This is the default configuration.
$\resizebox{4in}{!}{ \includegraphics{s_phys_pkgs/figs/s6t_32x32.ps} }$

Tiles can be selected from the topology to be omitted from being allocated memory and processors. This tuning is useful in ocean modeling for omitting tiles that fall entirely on land. The tiles omitted are specified in the file blanklist.txt by their tile number in the topology, separated by a newline.

6.2.4.4 exch2, SIZE.h, and Multiprocessing

Once the topology configuration files are created, the Fortran PARAMETERs in SIZE.h must be configured to match. Section 4.3.1 Specifying a decomposition provides a general description of domain decomposition within MITgcm and its relation to SIZE.h. The current section specifies constraints that the exch2 package imposes and describes how to enable parallel execution with MPI.

As in the general case, the parameters sNx and sNy define the size of the individual tiles, and so must be assigned the same respective values as tnx and tny in driver.m.

The halo width parameters OLx and OLy have no special bearing on exch2 and may be assigned as in the general case. The same holds for Nr, the number of vertical levels in the model.

The parameters nSx, nSy, nPx, and nPy relate to the number of tiles and how they are distributed on processors. When using exch2, the tiles are stored in the

dimension, and so nSy=1 in all cases. Since the tiles as configured by exch2 cannot be split up accross processors without regenerating the topology, nPy=1 as well.

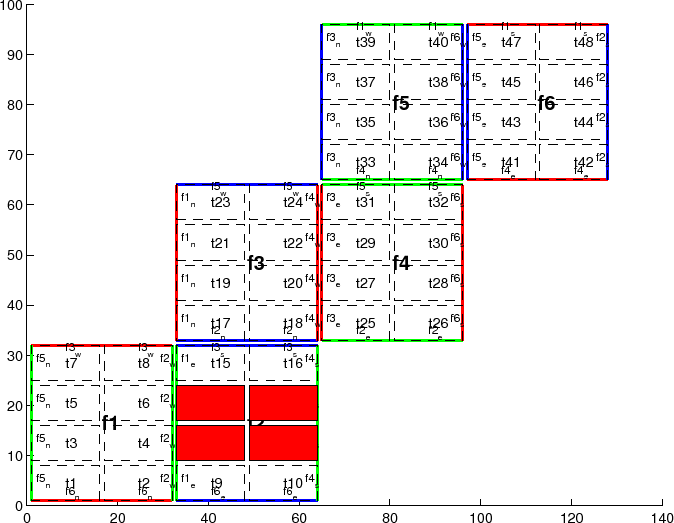
The number of tiles MITgcm allocates and how they are distributed between processors depends on nPx and nSx. nSx is the number of tiles per processor and nPx is the number of processors. The total number of tiles in the topology minus those listed in blanklist.txt must equal nSx*nPx. Note that in order to obtain maximum usage from a given number of processors in some cases, this restriction might entail sharing a processor with a tile that would otherwise be excluded because it is topographically outside of the domain and therefore in blanklist.txt. For example, suppose you have five processors and a domain decomposition of thirty-six tiles that allows you to exclude seven tiles. To evenly distribute the remaining twenty-nine tiles among five processors, you would have to run one ``dummy'' tile to make an even six tiles per processor. Such dummy tiles are not listed in blanklist.txt.

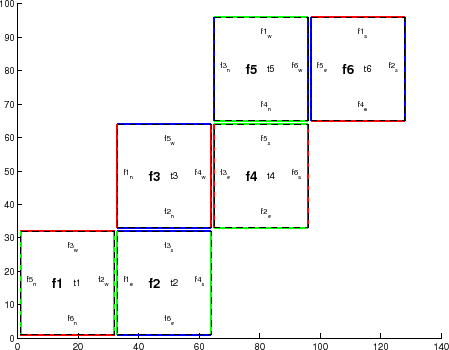
The following is an example of SIZE.h for the six-tile configuration illustrated in figure 6.4 running on one processor:

The following is an example for the forty-eight-tile topology in figure 6.2 running on six processors:

6.2.4.5 Key Variables

The descriptions of the variables are divided up into scalars, one-dimensional arrays indexed to the tile number, and two and three-dimensional arrays indexed to tile number and neighboring tile. This division reflects the functionality of these variables: The scalars are common to every part of the topology, the tile-indexed arrays to individual tiles, and the arrays indexed by tile and neighbor to relationships between tiles and their neighbors.

The number of tiles in a particular topology is set with the parameter NTILES, and the maximum number of neighbors of any tiles by MAX_NEIGHBOURS. These parameters are used for defining the size of the various one and two dimensional arrays that store tile parameters indexed to the tile number and are assigned in the files generated by driver.m.

The scalar parameters exch2_domain_nxt and exch2_domain_nyt express the number of tiles in the

and

global indices. For example, the default setup of six tiles (Fig. 6.4) has exch2_domain_nxt=6 and exch2_domain_nyt=1. A topology of forty-eight tiles, eight per subdomain (as in figure 6.2), will have exch2_domain_nxt=12 and exch2_domain_nyt=4. Note that these parameters express the tile layout in order to allow global data files that are tile-layout-neutral. They have no bearing on the internal storage of the arrays. The tiles are stored internally in a range from bi=(1:NTILES) in the

axis, and the

axis variable bj is assumed to equal 1 throughout the package.

The following arrays are of length NTILES and are indexed to the tile number, which is indicated in the diagrams with the notation t

. The indices are omitted in the descriptions.

The arrays exch2_tnx and exch2_tny express the

and

dimensions of each tile. At present for each tile exch2_tnx=sNx and exch2_tny=sNy, as assigned in SIZE.h and described in Section 6.2.4.4 exch2, SIZE.h, and Multiprocessing. Future releases of MITgcm may allow varying tile sizes.

The arrays exch2_tbasex and exch2_tbasey determine the tiles' Cartesian origin within a subdomain and locate the edges of different tiles relative to each other. As an example, in the default six-tile topology (Fig. 6.4) each index in these arrays is set to 0 since a tile occupies its entire subdomain. The twenty-four-tile case discussed above will have values of 0 or 16, depending on the quadrant of the tile within the subdomain. The elements of the arrays exch2_txglobalo and exch2_txglobalo are similar to exch2_tbasex and exch2_tbasey, but locate the tile edges within the global address space, similar to that used by global output and input files.

The array exch2_myFace contains the number of the subdomain of each tile, in a range (1:6) in the case of the standard cube topology and indicated by f

in figures 6.4 and 6.2. exch2_nNeighbours contains a count of the neighboring tiles each tile has, and sets the bounds for looping over neighboring tiles. exch2_tProc holds the process rank of each tile, and is used in interprocess communication.

The arrays exch2_isWedge, exch2_isEedge, exch2_isSedge, and exch2_isNedge are set to 1 if the indexed tile lies on the edge of its subdomain, 0 if not. The values are used within the topology generator to determine the orientation of neighboring tiles, and to indicate whether a tile lies on the corner of a subdomain. The latter case requires special exchange and numerical handling for the singularities at the eight corners of the cube.

The following arrays have vectors of length MAX_NEIGHBOURS and NTILES and describe the orientations between the the tiles.

The array exch2_neighbourId(a,T) holds the tile number Tn for each of the tile number T's neighboring tiles a. The neighbor tiles are indexed (1:exch2_nNeighbours(T)) in the order right to left on the north then south edges, and then top to bottom on the east then west edges.

The exch2_opposingSend_record(a,T) array holds the index b of the element in exch2_neighbourId(b,Tn) that holds the tile number T, given Tn=exch2_neighborId(a,T). In other words,

The arrays exch2_pi and exch2_pj specify the transformations of indices in exchanges between the neighboring tiles. These transformations are necessary in exchanges between subdomains because a horizontal dimension in one subdomain may map to other horizonal dimension in an adjacent subdomain, and may also have its indexing reversed. This swapping arises from the ``folding'' of two-dimensional arrays into a three-dimensional cube.

The dimensions of exch2_pi(t,N,T) and exch2_pj(t,N,T) are the neighbor ID N and the tile number T as explained above, plus a vector of length 2 containing transformation factors t. The first element of the transformation vector holds the factor to multiply the index in the same dimension, and the second element holds the the same for the orthogonal dimension. To clarify, exch2_pi(1,N,T) holds the mapping of the

axis index of tile T to the

axis of tile T's neighbor N, and exch2_pi(2,N,T) holds the mapping of T's

index to the neighbor N's

index.

One of the two elements of exch2_pi or exch2_pj for a given tile T and neighbor N will be 0, reflecting the fact that the two axes are orthogonal. The other element will be 1 or -1, depending on whether the axes are indexed in the same or opposite directions. For example, the transform vector of the arrays for all tile neighbors on the same subdomain will be (1,0), since all tiles on the same subdomain are oriented identically. An axis that corresponds to the orthogonal dimension with the same index direction in a particular tile-neighbor orientation will have (0,1). Those with the opposite index direction will have (0,-1) in order to reverse the ordering.

The arrays exch2_oi, exch2_oj, exch2_oi_f, and exch2_oj_f are indexed to tile number and neighbor and specify the relative offset within the subdomain of the array index of a variable going from a neighboring tile N to a local tile T. Consider T=1 in the six-tile topology (Fig. 6.4), where

The simplest case is exch2_oi(2,1), the southern neighbor, which is Tn=6. The axes of T and Tn have the same orientation and their

axes have the same origin, and so an exchange between the two requires no changes to the

index. For the western neighbor (Tn=5), code_oi(3,1)=32 since the x=0 vector on T corresponds to the y=32 vector on Tn. The eastern edge of T shows the reverse case (exch2_oi(4,1)=-32)), where x=32 on T exchanges with x=0 on Tn=2.

The most interesting case, where exch2_oi(1,1)=33 and Tn=3, involves a reversal of indices. As in every case, the offset exch2_oi is added to the original

index of T multiplied by the transformation factor exch2_pi(t,N,T). Here exch2_pi(1,1,1)=0 since the

axis of T is orthogonal to the

axis of Tn. exch2_pi(2,1,1)=-1 since the

axis of T corresponds to the

axis of Tn, but the index is reversed. The result is that the index of the northern edge of T, which runs (1:32), is transformed to (-1:-32). exch2_oi(1,1) is then added to this range to get back (32:1) - the index of the

axis of Tn relative to T. This transformation may seem overly convoluted for the six-tile case, but it is necessary to provide a general solution for various topologies.

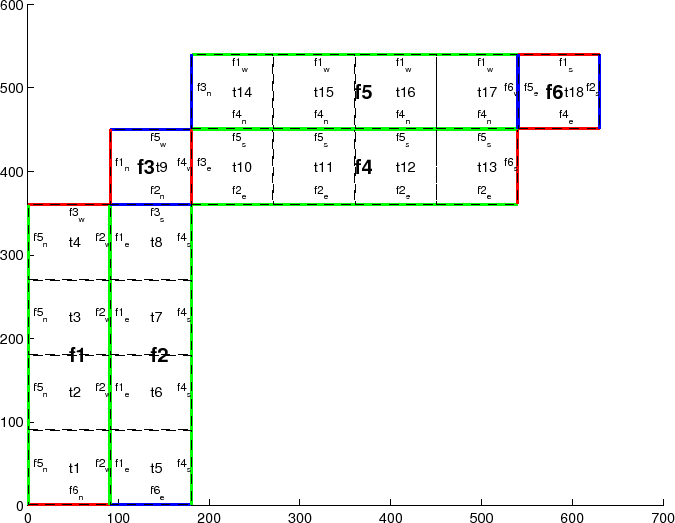
Finally, exch2_itlo_c, exch2_ithi_c, exch2_jtlo_c and exch2_jthi_c hold the location and index bounds of the edge segment of the neighbor tile N's subdomain that gets exchanged with the local tile T. To take the example of tile T=2 in the forty-eight-tile topology (Fig. 6.2):

Here N=4, indicating the western neighbor, which is Tn=1. Tn resides on the same subdomain as T, so the tiles have the same orientation and the same

and

axes. The

axis is orthogonal to the western edge and the tile is 16 points wide, so exch2_itlo_c and exch2_ithi_c indicate the column beyond Tn's eastern edge, in that tile's halo region. Since the border of the tiles extends through the entire height of the subdomain, the

axis bounds exch2_jtlo_c to exch2_jthi_c cover the height of (1:32), plus 1 in either direction to cover part of the halo.

For the north edge of the same tile T=2 where N=1 and the neighbor tile is Tn=5:

T's northern edge is parallel to the

axis, but since Tn's

axis corresponds to T's

axis, T's northern edge exchanges with Tn's western edge. The western edge of the tiles corresponds to the lower bound of the

axis, so exch2_itlo_c and exch2_ithi_c are 0, in the western halo region of Tn. The range of exch2_jtlo_c and exch2_jthi_c correspond to the width of T's northern edge, expanded by one into the halo.

6.2.4.6 Key Routines

Most of the subroutines particular to exch2 handle the exchanges themselves and are of the same format as those described in 4.3.3.3 Cube sphere communication. Like the original routines, they are written as templates which the local Makefile converts from RX into RL and RS forms.

The interfaces with the core model subroutines are EXCH_UV_XY_RX, EXCH_UV_XYZ_RX and EXCH_XY_RX. They override the standard exchange routines when genmake2 is run with exch2 option. They in turn call the local exch2 subroutines EXCH2_UV_XY_RX and EXCH2_UV_XYZ_RX for two and three-dimensional vector quantities, and EXCH2_XY_RX and EXCH2_XYZ_RX for two and three-dimensional scalar quantities. These subroutines set the dimensions of the area to be exchanged, call EXCH2_RX1_CUBE for scalars and EXCH2_RX2_CUBE for vectors, and then handle the singularities at the cube corners.

The separate scalar and vector forms of EXCH2_RX1_CUBE and EXCH2_RX2_CUBE reflect that the vector-handling subroutine needs to pass both the

and

components of the physical vectors. This swapping arises from the topological folding discussed above, where the

and

axes get swapped in some cases, and is not an issue with the scalar case. These subroutines call EXCH2_SEND_RX1 and EXCH2_SEND_RX2, which do most of the work using the variables discussed above.