|
 |
|||||||||||
 |
|
|||||||||||
 |
 |
|||||||||||
|
Next: 2.4 Pressure method with Up: 2. Discretization and Algorithm Previous: 2.2 Time-stepping Contents
|
|
The horizontal momentum and continuity equations for the ocean
(1.99 and 1.101), or for the atmosphere
(1.45 and 1.47), can be summarized by:
| (2.1) | |||
| (2.2) | |||
| 0 | (2.3) |
where we are adopting the oceanic notation for brevity. All terms in the momentum equations, except for surface pressure gradient, are encapsulated in the
Here,
As written here, terms on the LHS all involve time level
Substituting the two momentum equations into the depth integrated
continuity equation eliminates ![]() and
and ![]() yielding an
elliptic equation for
yielding an
elliptic equation for
![]() . Equations
2.5, 2.6 and
2.7 can then be re-arranged as follows:
. Equations
2.5, 2.6 and
2.7 can then be re-arranged as follows:
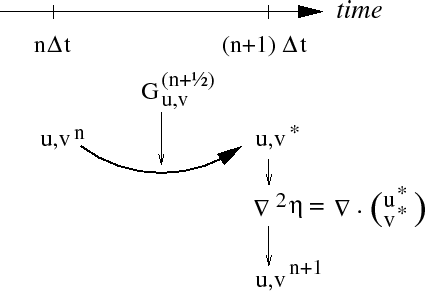
Equations 2.8 to 2.12, solved sequentially, represent the pressure method algorithm used in the model. The essence of the pressure method lies in the fact that any explicit prediction for the flow would lead to a divergence flow field so a pressure field must be found that keeps the flow non-divergent over each step of the integration. The particular location in time of the pressure field is somewhat ambiguous; in Fig. 2.1 we depicted as co-located with the future flow field (time level
The correspondence to the code is as follows:
- the prognostic phase, equations 2.8 and 2.9,
stepping forward
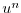 and
and 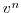 to
to 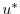 and
and 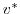 is coded in
TIMESTEP()
is coded in
TIMESTEP()
- the vertical integration,
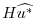 and
and
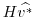 , divergence and inversion of the elliptic operator in
equation 2.10 is coded in
SOLVE_FOR_PRESSURE()
, divergence and inversion of the elliptic operator in
equation 2.10 is coded in
SOLVE_FOR_PRESSURE()
- finally, the new flow field at time level
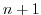 given by equations
2.11 and 2.12 is calculated in
CORRECTION_STEP().
given by equations
2.11 and 2.12 is calculated in
CORRECTION_STEP().
In general, the horizontal momentum time-stepping can contain some terms
that are treated implicitly in time,
such as the vertical viscosity when using the backward time-stepping scheme
(implicitViscosity
=.TRUE.).
The method used to solve those implicit terms is provided in
section 2.6, and modifies
equations 2.5 and 2.6 to
give:
| (2.13) | |||
| (2.14) |
Next: 2.4 Pressure method with Up: 2. Discretization and Algorithm Previous: 2.2 Time-stepping Contents mitgcm-support@mitgcm.org