Home Contact Us Site Map  
 
       
    next up previous contents
Next: 2.5 Explicit time-stepping: Adams-Bashforth Up: 2. Discretization and Algorithm Previous: 2.3 Pressure method with   Contents


2.4 Pressure method with implicit linear free-surface

The rigid-lid approximation filters out external gravity waves subsequently modifying the dispersion relation of barotropic Rossby waves. The discrete form of the elliptic equation has some zero eigen-values which makes it a potentially tricky or inefficient problem to solve.

The rigid-lid approximation can be easily replaced by a linearization of the free-surface equation which can be written:

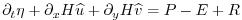$\displaystyle \partial_t \eta + \partial_x H \widehat{u} + \partial_y H \widehat{v} = P-E+R$ (2.15)

which differs from the depth integrated continuity equation with rigid-lid (2.4) by the time-dependent term and fresh-water source term.

Equation 2.7 in the rigid-lid pressure method is then replaced by the time discretization of 2.15 which is:

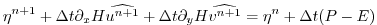$\displaystyle \eta^{n+1} + \Delta t \partial_x H \widehat{u^{n+1}} + \Delta t \partial_y H \widehat{v^{n+1}} = \eta^{n} + \Delta t ( P - E )$ (2.16)

where the use of flow at time level 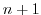$ n+1$ makes the method implicit and backward in time. This is the preferred scheme since it still filters the fast unresolved wave motions by damping them. A centered scheme, such as Crank-Nicholson (see section 2.10.1), would alias the energy of the fast modes onto slower modes of motion.

As for the rigid-lid pressure method, equations 2.5, 2.6 and 2.16 can be re-arranged as follows:

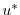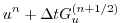$\displaystyle u^{*}$ $\displaystyle =$ $\displaystyle u^{n} + \Delta t G_u^{(n+1/2)}$ (2.17)
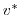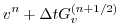$\displaystyle v^{*}$ $\displaystyle =$ $\displaystyle v^{n} + \Delta t G_v^{(n+1/2)}$ (2.18)
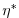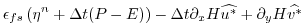$\displaystyle \eta^*$ $\displaystyle =$ $\displaystyle \epsilon_{fs} \left( \eta^{n} + \Delta t (P-E) \right)- \Delta t \partial_x H \widehat{u^{*}} + \partial_y H \widehat{v^{*}}$ (2.19)
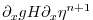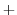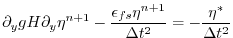$\displaystyle \partial_x g H \partial_x \eta^{n+1}$ $\displaystyle +$ $\displaystyle \partial_y g H \partial_y \eta^{n+1} - \frac{\epsilon_{fs} \eta^{n+1}}{\Delta t^2} = - \frac{\eta^*}{\Delta t^2}$ (2.20)
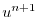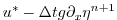$\displaystyle u^{n+1}$ $\displaystyle =$ $\displaystyle u^{*} - \Delta t g \partial_x \eta^{n+1}$ (2.21)
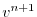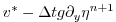$\displaystyle v^{n+1}$ $\displaystyle =$ $\displaystyle v^{*} - \Delta t g \partial_y \eta^{n+1}$ (2.22)

Equations 2.17 to 2.22, solved sequentially, represent the pressure method algorithm with a backward implicit, linearized free surface. The method is still formerly a pressure method because in the limit of large 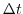$ \Delta t$ the rigid-lid method is recovered. However, the implicit treatment of the free-surface allows the flow to be divergent and for the surface pressure/elevation to respond on a finite time-scale (as opposed to instantly). 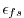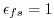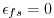To recover the rigid-lid formulation, we introduced a switch-like parameter, $ \epsilon_{fs}$ (freesurfFac), which selects between the free-surface and rigid-lid; $ \epsilon_{fs}=1$ allows the free-surface to evolve; $ \epsilon_{fs}=0$ imposes the rigid-lid. The evolution in time and location of variables is exactly as it was for the rigid-lid model so that Fig. 2.1 is still applicable. Similarly, the calling sequence, given in Fig. 2.2, is as for the pressure-method.

next up previous contents
Next: 2.5 Explicit time-stepping: Adams-Bashforth Up: 2. Discretization and Algorithm Previous: 2.3 Pressure method with   Contents
mitgcm-support@mitgcm.org
Copyright © 2006 Massachusetts Institute of Technology Last update 2011-01-09