2.2 Time-stepping

The equations of motion integrated by the model involve four prognostic equations for flow, 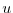and 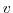, temperature, 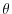, and salt/moisture, 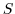, and three diagnostic equations for vertical flow, 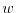, density/buoyancy, 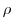/ 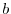, and pressure/geo-potential, 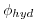. In addition, the surface pressure or height may by described by either a prognostic or diagnostic equation and if non-hydrostatics terms are included then a diagnostic equation for non-hydrostatic pressure is also solved. The combination of prognostic and diagnostic equations requires a model algorithm that can march forward prognostic variables while satisfying constraints imposed by diagnostic equations.

Since the model comes in several flavors and formulation, it would be confusing to present the model algorithm exactly as written into code along with all the switches and optional terms. Instead, we present the algorithm for each of the basic formulations which are:

1. the semi-implicit pressure method for hydrostatic equations with a rigid-lid, variables co-located in time and with Adams-Bashforth time-stepping,
2. as 1. but with an implicit linear free-surface,
3. as 1. or 2. but with variables staggered in time,
4. as 1. or 2. but with non-hydrostatic terms included,
5. as 2. or 3. but with non-linear free-surface.

In all the above configurations it is also possible to substitute the Adams-Bashforth with an alternative time-stepping scheme for terms evaluated explicitly in time. Since the over-arching algorithm is independent of the particular time-stepping scheme chosen we will describe first the over-arching algorithm, known as the pressure method, with a rigid-lid model in section 2.3. This algorithm is essentially unchanged, apart for some coefficients, when the rigid lid assumption is replaced with a linearized implicit free-surface, described in section 2.4. These two flavors of the pressure-method encompass all formulations of the model as it exists today. The integration of explicit in time terms is out-lined in section 2.5 and put into the context of the overall algorithm in sections 2.7 and 2.8. Inclusion of non-hydrostatic terms requires applying the pressure method in three dimensions instead of two and this algorithm modification is described in section 2.9. Finally, the free-surface equation may be treated more exactly, including non-linear terms, and this is described in section 2.10.2.

Copyright © 2006 Massachusetts Institute of Technology

Last update 2011-01-09