2.11.4 Horizontal grid

Figure 2.10: Staggering of horizontal grid descriptors (lengths and areas). The grid lines indicate the tracer cell boundaries and are the reference grid for all panels. a) The area of a tracer cell,

, is bordered by the lengths $\Delta x_g$ and $\Delta y_g$ . b) The area of a vorticity cell, $A_\zeta$ , is bordered by the lengths $\Delta x_c$ and $\Delta y_c$ . c) The area of a u cell,

, is bordered by the lengths $\Delta x_v$ and $\Delta y_f$ . d) The area of a v cell,

, is bordered by the lengths $\Delta x_f$ and $\Delta y_u$ .

a) $\resizebox{!}{2in}{ \includegraphics{s_algorithm/figs/hgrid-Ac.eps}}$	b) $\resizebox{!}{2in}{ \includegraphics{s_algorithm/figs/hgrid-Az.eps}}$
c) $\resizebox{!}{2in}{ \includegraphics{s_algorithm/figs/hgrid-Au.eps}}$	d) $\resizebox{!}{2in}{ \includegraphics{s_algorithm/figs/hgrid-Av.eps}}$

The model domain is decomposed into tiles and within each tile a quasi-regular grid is used. A tile is the basic unit of domain decomposition for parallelization but may be used whether parallelized or not; see section 4.2.4 for more details. Although the tiles may be patched together in an unstructured manner (i.e. irregular or non-tessilating pattern), the interior of tiles is a structured grid of quadrilateral cells. The horizontal coordinate system is orthogonal curvilinear meaning we can not necessarily treat the two horizontal directions as separable. Instead, each cell in the horizontal grid is described by the length of it's sides and it's area.

The grid information is quite general and describes any of the available coordinates systems, cartesian, spherical-polar or curvilinear. All that is necessary to distinguish between the coordinate systems is to initialize the grid data (descriptors) appropriately.

In the following, we refer to the orientation of quantities on the computational grid using geographic terminology such as points of the compass. This is purely for convenience but should note be confused with the actual geographic orientation of model quantities.

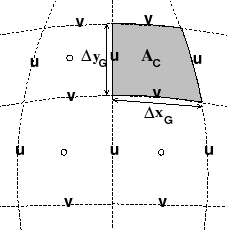
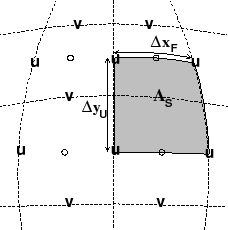
Fig. 2.10a shows the tracer cell (synonymous with the continuity cell). The length of the southern edge, $\Delta x_g$ , western edge, $\Delta y_g$ and surface area,

, presented in the vertical are stored in arrays DXg, DYg and rAc. The ``g'' suffix indicates that the lengths are along the defining grid boundaries. The ``c'' suffix associates the quantity with the cell centers. The quantities are staggered in space and the indexing is such that DXg(i,j) is positioned to the south of rAc(i,j) and DYg(i,j) positioned to the west.

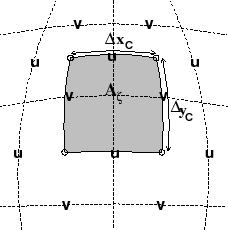
Fig. 2.10b shows the vorticity cell. The length of the southern edge, $\Delta x_c$ , western edge, $\Delta y_c$ and surface area, $A_\zeta$ , presented in the vertical are stored in arrays DXc, DYc and rAz. The ``z'' suffix indicates that the lengths are measured between the cell centers and the `` $\zeta$ '' suffix associates points with the vorticity points. The quantities are staggered in space and the indexing is such that DXc(i,j) is positioned to the north of rAc(i,j) and DYc(i,j) positioned to the east.

Fig. 2.10c shows the ``u'' or western (w) cell. The length of the southern edge, $\Delta x_v$ , eastern edge, $\Delta y_f$ and surface area,

, presented in the vertical are stored in arrays DXv, DYf and rAw. The ``v'' suffix indicates that the length is measured between the v-points, the ``f'' suffix indicates that the length is measured between the (tracer) cell faces and the ``w'' suffix associates points with the u-points (w stands for west). The quantities are staggered in space and the indexing is such that DXv(i,j) is positioned to the south of rAw(i,j) and DYf(i,j) positioned to the east.

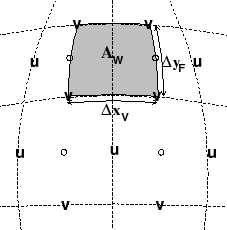
Fig. 2.10d shows the ``v'' or southern (s) cell. The length of the northern edge, $\Delta x_f$ , western edge, $\Delta y_u$ and surface area,

, presented in the vertical are stored in arrays DXf, DYu and rAs. The ``u'' suffix indicates that the length is measured between the u-points, the ``f'' suffix indicates that the length is measured between the (tracer) cell faces and the ``s'' suffix associates points with the v-points (s stands for south). The quantities are staggered in space and the indexing is such that DXf(i,j) is positioned to the north of rAs(i,j) and DYu(i,j) positioned to the west.

$\fbox{ \begin{minipage}{4.75in} {\em S/R INI\_CARTESIAN\_GRID} ({\em model/src/i... ...ta x_v$, $\Delta y_u$: {\bf DXv}, {\bf DYu} ({\em GRID.h}) \par \end{minipage} }$

2.11.4.1 Reciprocals of horizontal grid descriptors

Lengths and areas appear in the denominator of expressions as much as in the numerator. For efficiency and portability, we pre-calculate the reciprocal of the horizontal grid quantities so that in-line divisions can be avoided.

For each grid descriptor (array) there is a reciprocal named using the prefix RECIP_. This doubles the amount of storage in GRID.h but they are all only 2-D descriptors.

$\fbox{ \begin{minipage}{4.75in} {\em S/R INI\_MASKS\_ETC} ({\em model/src/ini\_m... ...u^{-1}$: {\bf RECIP\_DXv}, {\bf RECIP\_DYu} ({\em GRID.h}) \par \end{minipage} }$

2.11.4.2 Cartesian coordinates

Cartesian coordinates are selected when the logical flag usingCartesianGrid in namelist PARM04 is set to true. The grid spacing can be set to uniform via scalars dXspacing and dYspacing in namelist PARM04 or to variable resolution by the vectors DELX and DELY. Units are normally meters. Non-dimensional coordinates can be used by interpreting the gravitational constant as the Rayleigh number.

2.11.4.3 Spherical-polar coordinates

Spherical coordinates are selected when the logical flag usingSphericalPolarGrid in namelist PARM04 is set to true. The grid spacing can be set to uniform via scalars dXspacing and dYspacing in namelist PARM04 or to variable resolution by the vectors DELX and DELY. Units of these namelist variables are alway degrees. The horizontal grid descriptors are calculated from these namelist variables have units of meters.

2.11.4.4 Curvilinear coordinates

Curvilinear coordinates are selected when the logical flag usingCurvilinearGrid in namelist PARM04 is set to true. The grid spacing can not be set via the namelist. Instead, the grid descriptors are read from data files, one for each descriptor. As for other grids, the horizontal grid descriptors have units of meters.