Home Contact Us Site Map  
 
       
    next up previous contents
Next: 4.3.2 Starting the code Up: 4.3 Using the WRAPPER Previous: 4.3 Using the WRAPPER   Contents

Subsections


4.3.1 Specifying a domain decomposition

At its heart much of the WRAPPER works only in terms of a collection of tiles which are interconnected to each other. This is also true of application code operating within the WRAPPER. Application code is written as a series of compute operations, each of which operates on a single tile. If application code needs to perform operations involving data associated with another tile, it uses a WRAPPER function to obtain that data. The specification of how a global domain is constructed from tiles or alternatively how a global domain is decomposed into tiles is made in the file SIZE.h. This file defines the following parameters

\fbox{ \begin{minipage}{4.75in} Parameters: {\em sNx, sNy, OLx, OLy, nSx, nSy, nPx, nPy} \\ File: {\em model/inc/SIZE.h} \end{minipage}}

Together these parameters define a tiling decomposition of the style shown in figure 4.9. The parameters sNx and sNy define the size of an individual tile. The parameters OLx and OLy define the maximum size of the overlap extent. This must be set to the maximum width of the computation stencil that the numerical code finite-difference operations require between overlap region updates. The maximum overlap required by any of the operations in the MITgcm code distributed with this release is three grid points. This is set by the requirements of the $ \nabla^4$ dissipation and diffusion operator. Code modifications and enhancements that involve adding wide finite-difference stencils may require increasing OLx and OLy. Setting OLx and OLy to a too large value will decrease code performance (because redundant computations will be performed), however it will not cause any other problems.

Figure 4.9: The three level domain decomposition hierarchy employed by the WRAPPER. A domain is composed of tiles. Multiple tiles can be allocated to a single process. Multiple processes can exist, each with multiple tiles. Tiles within a process can be spread over multiple compute threads.
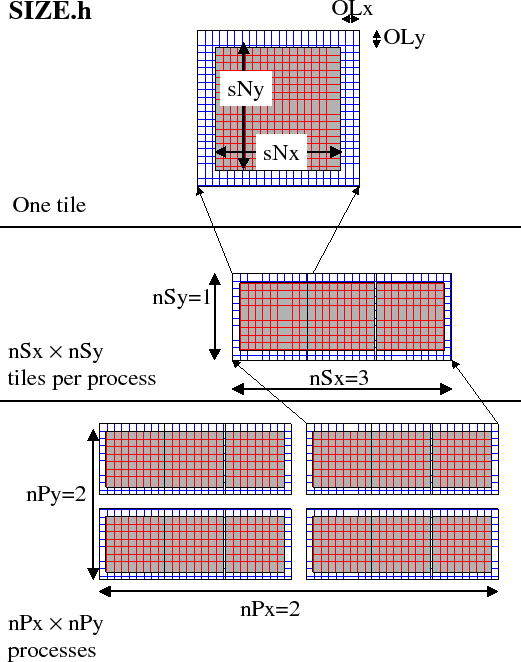
\resizebox{5in}{!}{ \includegraphics{s_software/figs/size_h.eps} }

The parameters nSx and nSy specify the number of tiles that will be created within a single process. Each of these tiles will have internal dimensions of sNx and sNy. If, when the code is executed, these tiles are allocated to different threads of a process that are then bound to different physical processors ( see the multi-threaded execution discussion in section 4.3.2 ) then computation will be performed concurrently on each tile. However, it is also possible to run the same decomposition within a process running a single thread on a single processor. In this case the tiles will be computed over sequentially. If the decomposition is run in a single process running multiple threads but attached to a single physical processor, then, in general, the computation for different tiles will be interleaved by system level software. This too is a valid mode of operation.

The parameters sNx, sNy, OLx, OLy, nSx andnSy are used extensively by numerical code. The settings of sNx, sNy, OLx and OLy are used to form the loop ranges for many numerical calculations and to provide dimensions for arrays holding numerical state. The nSx andnSy are used in conjunction with the thread number parameter myThid. Much of the numerical code operating within the WRAPPER takes the form 

      DO bj=myByLo(myThid),myByHi(myThid)
       DO bi=myBxLo(myThid),myBxHi(myThid)
          :
          a block of computations ranging 
          over 1,sNx +/- OLx and 1,sNy +/- OLy grid points
          :
       ENDDO
      ENDDO

      communication code to sum a number or maybe update
      tile overlap regions

      DO bj=myByLo(myThid),myByHi(myThid)
       DO bi=myBxLo(myThid),myBxHi(myThid)
          :
          another block of computations ranging 
          over 1,sNx +/- OLx and 1,sNy +/- OLy grid points
          :
       ENDDO
      ENDDO
The variables myBxLo(myThid), myBxHi(myThid), myByLo(myThid) and myByHi(myThid) set the bounds of the loops in bi and bj in this schematic. These variables specify the subset of the tiles in the range 1,nSx and 1,nSy that the logical processor bound to thread number myThid owns. The thread number variable myThid ranges from 1 to the total number of threads requested at execution time. For each value of myThid the loop scheme above will step sequentially through the tiles owned by that thread. However, different threads will have different ranges of tiles assigned to them, so that separate threads can compute iterations of the bi, bj loop concurrently. Within a bi, bj loop computation is performed concurrently over as many processes and threads as there are physical processors available to compute.

An exception to the the use of bi and bj in loops arises in the exchange routines used when the exch2 package is used with the cubed sphere. In this case bj is generally set to 1 and the loop runs from 1,bi. Within the loop bi is used to retrieve the tile number, which is then used to reference exchange parameters.

The amount of computation that can be embedded a single loop over bi and bj varies for different parts of the MITgcm algorithm. Figure 4.10 shows a code extract from the two-dimensional implicit elliptic solver. This portion of the code computes the l2Norm of a vector whose elements are held in the array cg2d_r writing the final result to scalar variable err. In this case, because the l2norm requires a global reduction, the bi,bj loop only contains one statement. This computation phase is then followed by a communication phase in which all threads and processes must participate. However, in other areas of the MITgcm code entries subsections of code are within a single bi,bj loop. For example the evaluation of all the momentum equation prognostic terms ( see S/R DYNAMICS()) is within a single bi,bj loop.

Figure 4.10: Example of numerical code for calculating the l2-norm of a vector within the WRAPPER. Notice that under the WRAPPER arrays such as cg2d_r have two extra trailing dimensions. These right most indices are tile indexes. Different threads with a single process operate on different ranges of tile index, as controlled by the settings of myByLo, myByHi, myBxLo and myBxHi.
\begin{figure}\begin{verbatim}REAL*8 cg2d_r(1-OLx:sNx+OLx,1-OLy:sNy+OLy,nSx,n... ... CALL GLOBAL_SUM_R8( err , myThid ) err = SQRT(err)\end{verbatim} \end{figure}

The final decomposition parameters are nPx and nPy. These parameters are used to indicate to the WRAPPER level how many processes (each with nSx$ \times $ nSy tiles) will be used for this simulation. This information is needed during initialization and during I/O phases. However, unlike the variables sNx, sNy, OLx, OLy, nSx and nSy the values of nPx and nPy are absent from the core numerical and support code.

4.3.1.1 Examples of SIZE.h specifications

The following different SIZE.h parameter setting illustrate how to interpret the values of sNx, sNy, OLx, OLy, nSx, nSy, nPx and nPy. 

  1.       PARAMETER (
     &           sNx =  90,
     &           sNy =  40,
     &           OLx =   3,
     &           OLy =   3,
     &           nSx =   1,
     &           nSy =   1,
     &           nPx =   1,
     &           nPy =   1)
    This sets up a single tile with x-dimension of ninety grid points, y-dimension of forty grid points, and x and y overlaps of three grid points each. 
  2.       PARAMETER (
     &           sNx =  45,
     &           sNy =  20,
     &           OLx =   3,
     &           OLy =   3,
     &           nSx =   1,
     &           nSy =   1,
     &           nPx =   2,
     &           nPy =   2)
    This sets up tiles with x-dimension of forty-five grid points, y-dimension of twenty grid points, and x and y overlaps of three grid points each. There are four tiles allocated to four separate processes (nPx=2,nPy=2) and arranged so that the global domain size is again ninety grid points in x and forty grid points in y. In general the formula for global grid size (held in model variables Nx and Ny) is 
                     Nx  = sNx*nSx*nPx
                 Ny  = sNy*nSy*nPy

  3.       PARAMETER (
     &           sNx =  90,
     &           sNy =  10,
     &           OLx =   3,
     &           OLy =   3,
     &           nSx =   1,
     &           nSy =   2,
     &           nPx =   1,
     &           nPy =   2)
    This sets up tiles with x-dimension of ninety grid points, y-dimension of ten grid points, and x and y overlaps of three grid points each. There are four tiles allocated to two separate processes (nPy=2) each of which has two separate sub-domains nSy=2, The global domain size is again ninety grid points in x and forty grid points in y. The two sub-domains in each process will be computed sequentially if they are given to a single thread within a single process. Alternatively if the code is invoked with multiple threads per process the two domains in y may be computed concurrently. 
  4.       PARAMETER (
     &           sNx =  32,
     &           sNy =  32,
     &           OLx =   3,
     &           OLy =   3,
     &           nSx =   6,
     &           nSy =   1,
     &           nPx =   1,
     &           nPy =   1)
    This sets up tiles with x-dimension of thirty-two grid points, y-dimension of thirty-two grid points, and x and y overlaps of three grid points each. There are six tiles allocated to six separate logical processors (nSx=6). This set of values can be used for a cube sphere calculation. Each tile of size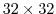 $ 32 \times 32$ represents a face of the cube. Initializing the tile connectivity correctly ( see section 4.3.3.3. allows the rotations associated with moving between the six cube faces to be embedded within the tile-tile communication code.

next up previous contents
Next: 4.3.2 Starting the code Up: 4.3 Using the WRAPPER Previous: 4.3 Using the WRAPPER   Contents
mitgcm-support@mitgcm.org
Copyright © 2006 Massachusetts Institute of Technology Last update 2018-01-23