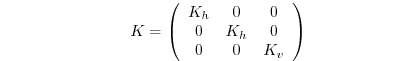|
|
|
|



Next: 1.3.8 Vector invariant form
Up: 1.3 Continuous equations in
Previous: 1.3.6 Finding the pressure
Contents
Subsections
The forcing terms
 on the rhs of the equations are provided by
`physics packages' and forcing packages. These are described later on.
on the rhs of the equations are provided by
`physics packages' and forcing packages. These are described later on.
Many forms of momentum dissipation are available in the model. Laplacian and
biharmonic frictions are commonly used:
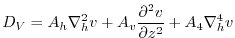 |
(1.41) |
where 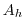 and
and 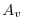 are (constant) horizontal and vertical viscosity
coefficients and
are (constant) horizontal and vertical viscosity
coefficients and 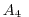 is the horizontal coefficient for biharmonic
friction. These coefficients are the same for all velocity components.
is the horizontal coefficient for biharmonic
friction. These coefficients are the same for all velocity components.
The mixing terms for the temperature and salinity equations have a similar
form to that of momentum except that the diffusion tensor can be
non-diagonal and have varying coefficients.
![$\displaystyle D_{T,S}=\nabla .[\underline{\underline{K}}\nabla (T,S)]+K_{4}\nabla _{h}^{4}(T,S)$](img261.png) |
(1.42) |
where
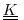 is the diffusion tensor and the
is the diffusion tensor and the 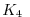 horizontal coefficient for biharmonic diffusion. In the simplest case where
the subgrid-scale fluxes of heat and salt are parameterized with constant
horizontal and vertical diffusion coefficients,
horizontal coefficient for biharmonic diffusion. In the simplest case where
the subgrid-scale fluxes of heat and salt are parameterized with constant
horizontal and vertical diffusion coefficients,
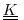 ,
reduces to a diagonal matrix with constant coefficients:
,
reduces to a diagonal matrix with constant coefficients:
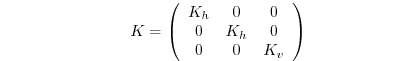 |
(1.43) |
where 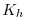 and
and 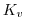 are the horizontal and vertical diffusion
coefficients. These coefficients are the same for all tracers (temperature,
salinity ... ).
are the horizontal and vertical diffusion
coefficients. These coefficients are the same for all tracers (temperature,
salinity ... ).



Next: 1.3.8 Vector invariant form
Up: 1.3 Continuous equations in
Previous: 1.3.6 Finding the pressure
Contents
mitgcm-support@mitgcm.org
| Copyright © 2006
Massachusetts Institute of Technology |
Last update 2018-01-23 |
 |
|