|
 |
|||||||||||
 |
|
|||||||||||
 |
 |
|||||||||||
|
Next: 6.2.5 Gridalt - Alternate Up: 6.2 Packages Related to Previous: 6.2.3 FFT Filtering Code Contents Subsections
|
|
|
|
Tiles can be selected from the topology to be omitted from being
allocated memory and processors. This tuning is useful in ocean
modeling for omitting tiles that fall entirely on land. The tiles
omitted are specified in the file
blanklist.txt
by their tile number in the topology, separated by a newline.
6.2.4.4 exch2, SIZE.h, and Multiprocessing
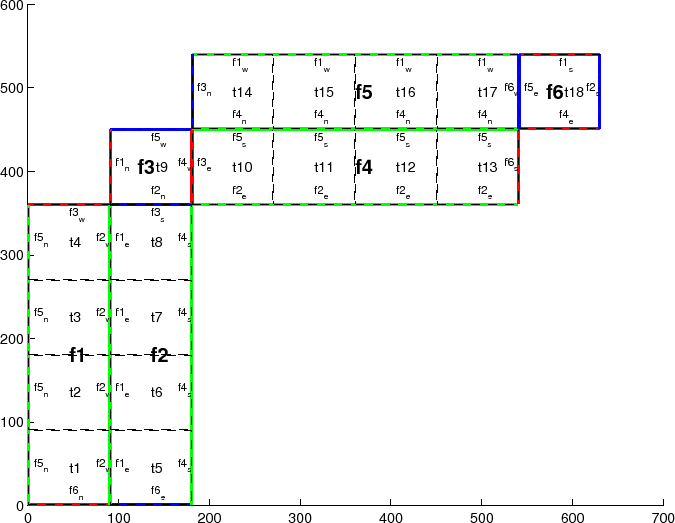
Once the topology configuration files are created, the Fortran PARAMETERs in SIZE.h must be configured to match. Section 4.3.1 Specifying a decomposition provides a general description of domain decomposition within MITgcm and its relation to SIZE.h. The current section specifies constraints that the exch2 package imposes and describes how to enable parallel execution with MPI.
As in the general case, the parameters sNx and sNy define the size of the individual tiles, and so must be assigned the same respective values as tnx and tny in driver.m.
The halo width parameters OLx and OLy have no special bearing on exch2 and may be assigned as in the general case. The same holds for Nr, the number of vertical levels in the model.
The parameters nSx, nSy,
nPx, and nPy
relate to the number of
tiles and how they are distributed on processors. When using exch2,
the tiles are stored in the ![]() dimension, and so
nSy=1 in all cases. Since the tiles as
configured by exch2 cannot be split up accross processors without
regenerating the topology, nPy=1 as well.
dimension, and so
nSy=1 in all cases. Since the tiles as
configured by exch2 cannot be split up accross processors without
regenerating the topology, nPy=1 as well.
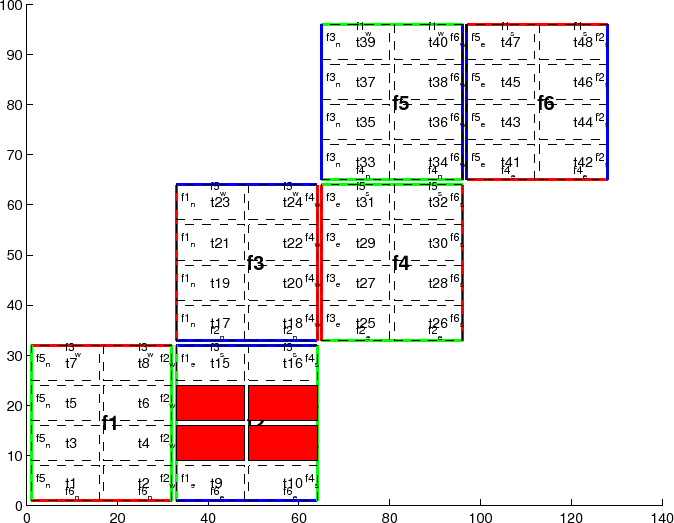
The number of tiles MITgcm allocates and how they are distributed between processors depends on nPx and nSx. nSx is the number of tiles per processor and nPx is the number of processors. The total number of tiles in the topology minus those listed in blanklist.txt must equal nSx*nPx. Note that in order to obtain maximum usage from a given number of processors in some cases, this restriction might entail sharing a processor with a tile that would otherwise be excluded because it is topographically outside of the domain and therefore in blanklist.txt. For example, suppose you have five processors and a domain decomposition of thirty-six tiles that allows you to exclude seven tiles. To evenly distribute the remaining twenty-nine tiles among five processors, you would have to run one ``dummy'' tile to make an even six tiles per processor. Such dummy tiles are not listed in blanklist.txt.
The following is an example of SIZE.h for the six-tile configuration illustrated in figure 6.4 running on one processor:
PARAMETER (
& sNx = 32,
& sNy = 32,
& OLx = 2,
& OLy = 2,
& nSx = 6,
& nSy = 1,
& nPx = 1,
& nPy = 1,
& Nx = sNx*nSx*nPx,
& Ny = sNy*nSy*nPy,
& Nr = 5)
The following is an example for the forty-eight-tile topology in figure 6.2 running on six processors:
PARAMETER (
& sNx = 16,
& sNy = 8,
& OLx = 2,
& OLy = 2,
& nSx = 8,
& nSy = 1,
& nPx = 6,
& nPy = 1,
& Nx = sNx*nSx*nPx,
& Ny = sNy*nSy*nPy,
& Nr = 5)
6.2.4.5 Key Variables
The descriptions of the variables are divided up into scalars,
one-dimensional arrays indexed to the tile number, and two and
three-dimensional arrays indexed to tile number and neighboring tile.
This division reflects the functionality of these variables: The
scalars are common to every part of the topology, the tile-indexed
arrays to individual tiles, and the arrays indexed by tile and
neighbor to relationships between tiles and their neighbors.
Scalars:
The number of tiles in a particular topology is set with the parameter
NTILES, and the maximum number of neighbors of any tiles by
MAX_NEIGHBOURS. These parameters are used for defining the
size of the various one and two dimensional arrays that store tile
parameters indexed to the tile number and are assigned in the files
generated by driver.m.
The scalar parameters exch2_domain_nxt
and exch2_domain_nyt
express the number
of tiles in the ![]() and
and ![]() global indices. For example, the default
setup of six tiles (Fig. 6.4) has
exch2_domain_nxt=6 and exch2_domain_nyt=1. A
topology of forty-eight tiles, eight per subdomain (as in figure
6.2), will have exch2_domain_nxt=12 and
exch2_domain_nyt=4. Note that these parameters express the
tile layout in order to allow global data files that are tile-layout-neutral.
They have no bearing on the internal storage of the arrays. The tiles
are stored internally in a range from bi=(1:NTILES) in the
global indices. For example, the default
setup of six tiles (Fig. 6.4) has
exch2_domain_nxt=6 and exch2_domain_nyt=1. A
topology of forty-eight tiles, eight per subdomain (as in figure
6.2), will have exch2_domain_nxt=12 and
exch2_domain_nyt=4. Note that these parameters express the
tile layout in order to allow global data files that are tile-layout-neutral.
They have no bearing on the internal storage of the arrays. The tiles
are stored internally in a range from bi=(1:NTILES) in the
![]() axis, and the
axis, and the ![]() axis variable bj
is assumed to
equal 1 throughout the package.
axis variable bj
is assumed to
equal 1 throughout the package.
Arrays indexed to tile number:
The following arrays are of length NTILES and are indexed to
the tile number, which is indicated in the diagrams with the notation
t![]() . The indices are omitted in the descriptions.
. The indices are omitted in the descriptions.
The arrays exch2_tnx
and
exch2_tny
express the ![]() and
and ![]() dimensions of
each tile. At present for each tile exch2_tnx=sNx and
exch2_tny=sNy, as assigned in SIZE.h and described in
Section 6.2.4.4 exch2, SIZE.h, and
Multiprocessing. Future releases of MITgcm may allow varying tile
sizes.
dimensions of
each tile. At present for each tile exch2_tnx=sNx and
exch2_tny=sNy, as assigned in SIZE.h and described in
Section 6.2.4.4 exch2, SIZE.h, and
Multiprocessing. Future releases of MITgcm may allow varying tile
sizes.
The arrays exch2_tbasex
and
exch2_tbasey
determine the tiles'
Cartesian origin within a subdomain
and locate the edges of different tiles relative to each other. As
an example, in the default six-tile topology (Fig. 6.4)
each index in these arrays is set to 0 since a tile occupies
its entire subdomain. The twenty-four-tile case discussed above will
have values of 0 or 16, depending on the quadrant of the
tile within the subdomain. The elements of the arrays
exch2_txglobalo
and
exch2_txglobalo
are similar to
exch2_tbasex
and
exch2_tbasey, but locate the tile edges within the
global address space, similar to that used by global output and input
files.
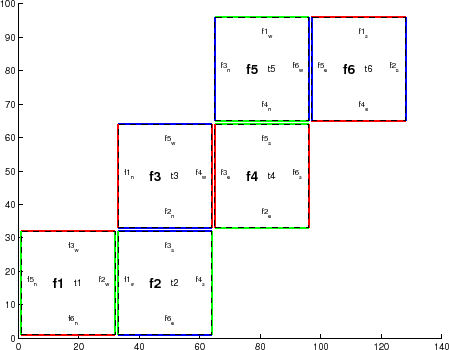
The array exch2_myFace
contains the number of
the subdomain of each tile, in a range (1:6) in the case of the
standard cube topology and indicated by f![]() in
figures 6.4 and
6.2. exch2_nNeighbours
contains a count of the neighboring tiles each tile has, and sets
the bounds for looping over neighboring tiles.
exch2_tProc
holds the process rank of each
tile, and is used in interprocess communication.
in
figures 6.4 and
6.2. exch2_nNeighbours
contains a count of the neighboring tiles each tile has, and sets
the bounds for looping over neighboring tiles.
exch2_tProc
holds the process rank of each
tile, and is used in interprocess communication.
The arrays exch2_isWedge,
exch2_isEedge,
exch2_isSedge, and
exch2_isNedge
are set to 1 if the
indexed tile lies on the edge of its subdomain, 0 if
not. The values are used within the topology generator to determine
the orientation of neighboring tiles, and to indicate whether a tile
lies on the corner of a subdomain. The latter case requires special
exchange and numerical handling for the singularities at the eight
corners of the cube.
Arrays Indexed to Tile Number and Neighbor:
The following arrays have vectors of length MAX_NEIGHBOURS and
NTILES and describe the orientations between the the tiles.
The array exch2_neighbourId(a,T) holds the tile number
Tn for each of the tile number T's neighboring tiles
a. The neighbor tiles are indexed
(1:exch2_nNeighbours(T)) in the order right to left on the
north then south edges, and then top to bottom on the east then west
edges.
The exch2_opposingSend_record(a,T) array holds the index b of the element in exch2_neighbourId(b,Tn) that holds the tile number T, given Tn=exch2_neighborId(a,T). In other words,
exch2_neighbourId( exch2_opposingSend_record(a,T),
exch2_neighbourId(a,T) ) = T
This provides a back-reference from the neighbor tiles.
The arrays exch2_pi
and
exch2_pj
specify the transformations of indices
in exchanges between the neighboring tiles. These transformations are
necessary in exchanges between subdomains because a horizontal dimension
in one subdomain
may map to other horizonal dimension in an adjacent subdomain, and
may also have its indexing reversed. This swapping arises from the
``folding'' of two-dimensional arrays into a three-dimensional
cube.
The dimensions of exch2_pi(t,N,T) and exch2_pj(t,N,T)
are the neighbor ID N and the tile number T as explained
above, plus a vector of length 2 containing transformation
factors t. The first element of the transformation vector
holds the factor to multiply the index in the same dimension, and the
second element holds the the same for the orthogonal dimension. To
clarify, exch2_pi(1,N,T) holds the mapping of the ![]() axis
index of tile T to the
axis
index of tile T to the ![]() axis of tile T's neighbor
N, and exch2_pi(2,N,T) holds the mapping of T's
axis of tile T's neighbor
N, and exch2_pi(2,N,T) holds the mapping of T's
![]() index to the neighbor N's
index to the neighbor N's ![]() index.
index.
One of the two elements of exch2_pi or exch2_pj for a
given tile T and neighbor N will be 0, reflecting
the fact that the two axes are orthogonal. The other element will be
1 or -1, depending on whether the axes are indexed in
the same or opposite directions. For example, the transform vector of
the arrays for all tile neighbors on the same subdomain will be
(1,0), since all tiles on the same subdomain are oriented
identically. An axis that corresponds to the orthogonal dimension
with the same index direction in a particular tile-neighbor
orientation will have (0,1). Those with the opposite index
direction will have (0,-1) in order to reverse the ordering.
The arrays exch2_oi, exch2_oj, exch2_oi_f, and exch2_oj_f are indexed to tile number and neighbor and specify the relative offset within the subdomain of the array index of a variable going from a neighboring tile N to a local tile T. Consider T=1 in the six-tile topology (Fig. 6.4), where
exch2_oi(1,1)=33
exch2_oi(2,1)=0
exch2_oi(3,1)=32
exch2_oi(4,1)=-32
The simplest case is exch2_oi(2,1), the southern neighbor,
which is Tn=6. The axes of T and Tn have the
same orientation and their ![]() axes have the same origin, and so an
exchange between the two requires no changes to the
axes have the same origin, and so an
exchange between the two requires no changes to the ![]() index. For
the western neighbor (Tn=5), code_oi(3,1)=32 since the
x=0 vector on T corresponds to the y=32 vector on
Tn. The eastern edge of T shows the reverse case
(exch2_oi(4,1)=-32)), where x=32 on T exchanges
with x=0 on Tn=2.
index. For
the western neighbor (Tn=5), code_oi(3,1)=32 since the
x=0 vector on T corresponds to the y=32 vector on
Tn. The eastern edge of T shows the reverse case
(exch2_oi(4,1)=-32)), where x=32 on T exchanges
with x=0 on Tn=2.
The most interesting case, where exch2_oi(1,1)=33 and
Tn=3, involves a reversal of indices. As in every case, the
offset exch2_oi is added to the original ![]() index of T
multiplied by the transformation factor exch2_pi(t,N,T). Here
exch2_pi(1,1,1)=0 since the
index of T
multiplied by the transformation factor exch2_pi(t,N,T). Here
exch2_pi(1,1,1)=0 since the ![]() axis of T is orthogonal
to the
axis of T is orthogonal
to the ![]() axis of Tn. exch2_pi(2,1,1)=-1 since the
axis of Tn. exch2_pi(2,1,1)=-1 since the
![]() axis of T corresponds to the
axis of T corresponds to the ![]() axis of Tn, but the
index is reversed. The result is that the index of the northern edge
of T, which runs (1:32), is transformed to
(-1:-32). exch2_oi(1,1) is then added to this range to
get back (32:1) - the index of the
axis of Tn, but the
index is reversed. The result is that the index of the northern edge
of T, which runs (1:32), is transformed to
(-1:-32). exch2_oi(1,1) is then added to this range to
get back (32:1) - the index of the ![]() axis of Tn
relative to T. This transformation may seem overly convoluted
for the six-tile case, but it is necessary to provide a general
solution for various topologies.
axis of Tn
relative to T. This transformation may seem overly convoluted
for the six-tile case, but it is necessary to provide a general
solution for various topologies.
Finally, exch2_itlo_c,
exch2_ithi_c,
exch2_jtlo_c
and
exch2_jthi_c
hold the location and index
bounds of the edge segment of the neighbor tile N's subdomain
that gets exchanged with the local tile T. To take the example
of tile T=2 in the forty-eight-tile topology
(Fig. 6.2):
exch2_itlo_c(4,2)=17
exch2_ithi_c(4,2)=17
exch2_jtlo_c(4,2)=0
exch2_jthi_c(4,2)=33
Here N=4, indicating the western neighbor, which is
Tn=1. Tn resides on the same subdomain as T, so
the tiles have the same orientation and the same ![]() and
and ![]() axes.
The
axes.
The ![]() axis is orthogonal to the western edge and the tile is 16
points wide, so exch2_itlo_c and exch2_ithi_c
indicate the column beyond Tn's eastern edge, in that tile's
halo region. Since the border of the tiles extends through the entire
height of the subdomain, the
axis is orthogonal to the western edge and the tile is 16
points wide, so exch2_itlo_c and exch2_ithi_c
indicate the column beyond Tn's eastern edge, in that tile's
halo region. Since the border of the tiles extends through the entire
height of the subdomain, the ![]() axis bounds exch2_jtlo_c to
exch2_jthi_c cover the height of (1:32), plus 1 in
either direction to cover part of the halo.
axis bounds exch2_jtlo_c to
exch2_jthi_c cover the height of (1:32), plus 1 in
either direction to cover part of the halo.
For the north edge of the same tile T=2 where N=1 and the neighbor tile is Tn=5:
exch2_itlo_c(1,2)=0
exch2_ithi_c(1,2)=0
exch2_jtlo_c(1,2)=0
exch2_jthi_c(1,2)=17
T's northern edge is parallel to the ![]() axis, but since
Tn's
axis, but since
Tn's ![]() axis corresponds to T's
axis corresponds to T's ![]() axis, T's
northern edge exchanges with Tn's western edge. The western
edge of the tiles corresponds to the lower bound of the
axis, T's
northern edge exchanges with Tn's western edge. The western
edge of the tiles corresponds to the lower bound of the ![]() axis, so
exch2_itlo_c and exch2_ithi_c are 0, in the
western halo region of Tn. The range of
exch2_jtlo_c and exch2_jthi_c correspond to the
width of T's northern edge, expanded by one into the halo.
axis, so
exch2_itlo_c and exch2_ithi_c are 0, in the
western halo region of Tn. The range of
exch2_jtlo_c and exch2_jthi_c correspond to the
width of T's northern edge, expanded by one into the halo.
6.2.4.6 Key Routines
Most of the subroutines particular to exch2 handle the exchanges
themselves and are of the same format as those described in
4.3.3.3 Cube sphere
communication. Like the original routines, they are written as
templates which the local Makefile converts from RX into
RL and RS forms.
The interfaces with the core model subroutines are
EXCH_UV_XY_RX, EXCH_UV_XYZ_RX and
EXCH_XY_RX. They override the standard exchange routines
when genmake2 is run with exch2 option. They in turn
call the local exch2 subroutines EXCH2_UV_XY_RX and
EXCH2_UV_XYZ_RX for two and three-dimensional vector
quantities, and EXCH2_XY_RX and EXCH2_XYZ_RX for two
and three-dimensional scalar quantities. These subroutines set the
dimensions of the area to be exchanged, call EXCH2_RX1_CUBE
for scalars and EXCH2_RX2_CUBE for vectors, and then handle
the singularities at the cube corners.
The separate scalar and vector forms of EXCH2_RX1_CUBE and
EXCH2_RX2_CUBE reflect that the vector-handling subroutine
needs to pass both the ![]() and
and ![]() components of the physical vectors.
This swapping arises from the topological folding discussed above, where the
components of the physical vectors.
This swapping arises from the topological folding discussed above, where the
![]() and
and ![]() axes get swapped in some cases, and is not an
issue with the scalar case. These subroutines call
EXCH2_SEND_RX1 and EXCH2_SEND_RX2, which do most of
the work using the variables discussed above.
axes get swapped in some cases, and is not an
issue with the scalar case. These subroutines call
EXCH2_SEND_RX1 and EXCH2_SEND_RX2, which do most of
the work using the variables discussed above.
6.2.4.7 Experiments and tutorials that use exch2
- Held Suarez tutorial, in tutorial_held_suarez_cs verification directory, described in section 3.14
Next: 6.2.5 Gridalt - Alternate Up: 6.2 Packages Related to Previous: 6.2.3 FFT Filtering Code Contents mitgcm-support@mitgcm.org