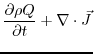Home Contact Us Site Map  
 
       
    next up previous contents
Next: 8. Ocean State Estimation Up: 7.7 Potential vorticity Matlab Previous: 7.7.4 Technical details   Contents

Subsections


7.7.5 Notes on the flux form of the PV equation and vertical PV fluxes

7.7.5.1 Flux form of the PV equation

The conservative flux form of the potential vorticity equation is:
$\displaystyle \frac{\partial \rho Q}{\partial t} + \nabla \cdot \vec{J}$ $\displaystyle =$ 0 (7.11)

where the potential vorticity $ Q$ is given by the Eq.7.3.

The generalized flux vector of potential vorticity is:

$\displaystyle \vec{J}$ $\displaystyle =$ $\displaystyle \rho Q \vec{u} + \vec{N_Q}$ (7.12)

which allows to rewrite Eq.7.11 as:
$\displaystyle \frac{DQ}{dt}$ $\displaystyle =$ $\displaystyle -\frac{1}{\rho}\nabla\cdot\vec{N_Q}$ (7.13)

where the nonadvective PV flux $ \vec{N_Q}$ is given by:
$\displaystyle \vec{N_Q}$ $\displaystyle =$ $\displaystyle -\frac{\rho_0}{g}B\vec{\omega_a} + \vec{F}\times\nabla\sigma_\theta$ (7.14)

Its first component is linked to the buoyancy forcing7.1:

$\displaystyle B$ $\displaystyle =$ $\displaystyle -\frac{g}{\rho_o}\frac{D \sigma_\theta}{dt}$ (7.16)

and the second one to the nonconservative body forces per unit mass:
$\displaystyle \vec{F}$ $\displaystyle =$ $\displaystyle \frac{D \vec{u}}{dt} + 2\Omega\times\vec{u} + \nabla p$ (7.17)

7.7.5.2 Determining the PV flux at the ocean's surface

In the context of mode water study, we're particularly interested in how the PV may be reduced by surface PV fluxes because a mode water is characterised by a low PV level. Considering the volume limited by two $ iso-\sigma_\theta$ , PV flux is limited to surface processes and then vertical component of $ \vec{N_Q}$ . It is supposed that $ B$ and $ \vec{F}$ will only be nonzero in the mixed layer (of depth $ h$ and variable density $ \sigma_m$ ) exposed to mechanical forcing by the wind and buoyancy fluxes through the ocean's surface.

Given the assumption of a mechanical forcing confined to a thin surface Ekman layer (of depth $ \delta_e$ , eventually computed by the package) and of hydrostatic and geostrophic balances, we can write:

$\displaystyle \vec{u_g}$ $\displaystyle =$ $\displaystyle \frac{1}{\rho f} \vec{k}\times\nabla p$ (7.18)
$\displaystyle \frac{\partial p_m}{\partial z}$ $\displaystyle =$ $\displaystyle -\sigma_m g$ (7.19)
$\displaystyle \frac{\partial \sigma_m}{\partial t} + \vec{u}_m\cdot\nabla\sigma_m$ $\displaystyle =$ $\displaystyle -\frac{\rho_0}{g}B$ (7.20)

where:
$\displaystyle \vec{u}_m$ $\displaystyle =$ $\displaystyle \vec{u}_g + \vec{u}_{Ek} + o(R_o)$ (7.21)

is the full velocity field composed by the geostrophic current $ \vec{u}_g$ and the Ekman drift:
$\displaystyle \vec{u}_{Ek}$ $\displaystyle =$ $\displaystyle -\frac{1}{\rho f}\vec{k}\times\frac{\partial \tau}{\partial z}$ (7.22)

(where $ \tau$ is the wind stress) and last by other ageostrophic components of $ o(R_o)$ which are neglected.

Partitioning the buoyancy forcing as:

$\displaystyle B$ $\displaystyle =$ $\displaystyle B_g + B_{Ek}$ (7.23)

and using Eq.7.21 and Eq.7.22, the Eq.7.20 becomes:
$\displaystyle \frac{\partial \sigma_m}{\partial t} + \vec{u}_g\cdot\nabla\sigma_m$ $\displaystyle =$ $\displaystyle -\frac{\rho_0}{g} B_g$ (7.24)

revealing the "wind-driven buoyancy forcing":
$\displaystyle B_{Ek}$ $\displaystyle =$ $\displaystyle \frac{g}{\rho_0}\frac{1}{\rho f}\left(\vec{k}\times\frac{\partial \tau}{\partial z}\right)\cdot\nabla\sigma_m$ (7.25)

Note that since:
$\displaystyle \frac{\partial B_g}{\partial z}$ $\displaystyle =$ $\displaystyle \frac{\partial}{\partial z}\left(-\frac{g}{\rho_0}\vec{u_g}\cdot\... ...-\frac{g}{\rho_0}\frac{\partial \vec{u_g}}{\partial z}\cdot\nabla\sigma_m = 0$ (7.26)

$ B_g$ must be uniform throughout the depth of the mixed layer and then being related to the surface buoyancy flux by integrating Eq.7.23 through the mixed layer:
$\displaystyle \int_{-h}^0B\,dz$ $\displaystyle =\, hB_g + \int_{-h}^0B_{Ek}\,dz \,=$ $\displaystyle \mathcal{B}_{in}$ (7.27)

where $ \mathcal{B}_{in}$ is the vertically integrated surface buoyancy (in)flux:
$\displaystyle \mathcal{B}_{in}$ $\displaystyle =$ $\displaystyle \frac{g}{\rho_o}\left( \frac{\alpha Q_{net}}{C_w} - \rho_0\beta S_{net}\right)$ (7.28)

with $ \alpha\simeq 2.5\times10^{-4}\, K^{-1}$ the thermal expansion coefficient (computed by the package otherwise), $ C_w=4187J.kg^{-1}.K^{-1}$ the specific heat of seawater, $ Q_{net}[W.m^{-2}]$ the net heat surface flux (positive downward, warming the ocean), $ \beta[PSU^{-1}]$ the saline contraction coefficient, and $ S_{net}=S*(E-P)[PSU.m.s^{-1}]$ the net freshwater surface flux with $ S[PSU]$ the surface salinity and $ (E-P)[m.s^{-1}]$ the fresh water flux.

Introducing the body force in the Ekman layer:

$\displaystyle F_z$ $\displaystyle =$ $\displaystyle \frac{1}{\rho}\frac{\partial \tau}{\partial z}$ (7.29)

the vertical component of Eq.7.14 is:
$\displaystyle \vec{N_Q}_z$ $\displaystyle =$ $\displaystyle -\frac{\rho_0}{g}(B_g+B_{Ek})\omega_z + \frac{1}{\rho} \left( \frac{\partial \tau}{\partial z}\times\nabla\sigma_\theta \right)\cdot\vec{k}$  
  $\displaystyle =$ $\displaystyle -\frac{\rho_0}{g}B_g\omega_z -\frac{\rho_0}{g} \left(\frac{g}{\... ...( \frac{\partial \tau}{\partial z}\times\nabla\sigma_\theta \right)\cdot\vec{k}$  
  $\displaystyle =$ $\displaystyle -\frac{\rho_0}{g}B_g\omega_z + \left(1-\frac{\omega_z}{f}\right)... ...\frac{\partial \tau}{\partial z} \times\nabla\sigma_\theta \right)\cdot\vec{k}$ (7.30)

and given the assumption that $ \omega_z\simeq f$ , the second term vanishes and we obtain:
$\displaystyle \vec{N_Q}_z$ $\displaystyle =$ $\displaystyle -\frac{\rho_0}{g}f B_g %\label{sec:diag:pv:eq12} $ (7.31)

Note that the wind-stress forcing does not appear explicitly here but is implicit in $ B_g$ through Eq.7.27: the buoyancy forcing $ B_g$ is determined by the difference between the integrated surface buoyancy flux $ \mathcal{B}_{in}$ and the integrated "wind-driven buoyancy forcing":
$\displaystyle B_g$ $\displaystyle =$ $\displaystyle \frac{1}{h}\left( \mathcal{B}_{in} - \int_{-h}^0B_{Ek}dz \right)$  
  $\displaystyle =$ $\displaystyle \frac{1}{h}\frac{g}{\rho_0}\left( \frac{\alpha Q_{net}}{C_w} - \r... ...1}{\rho f}\vec{k}\times \frac{\partial \tau}{\partial z} \cdot\nabla\sigma_m dz$  
  $\displaystyle =$ $\displaystyle \frac{1}{h}\frac{g}{\rho_0}\left( \frac{\alpha Q_{net}}{C_w} - \r... ...- \frac{g}{\rho_0}\frac{1}{\rho f \delta_e}\vec{k}\times\tau\cdot\nabla\sigma_m$ (7.32)

Finally, from Eq.7.14, the vertical surface flux of PV may be written as:
$\displaystyle \vec{N_Q}_z$ $\displaystyle =$ $\displaystyle J^B_z + J^F_z$ (7.33)
$\displaystyle J^B_z$ $\displaystyle =$ $\displaystyle -\frac{f}{h}\left( \frac{\alpha Q_{net}}{C_w}-\rho_0 \beta S_{net}\right)$ (7.34)
$\displaystyle J^F_z$ $\displaystyle =$ $\displaystyle \frac{1}{\rho\delta_e} \vec{k}\times\tau\cdot\nabla\sigma_m$ (7.35)

next up previous contents
Next: 8. Ocean State Estimation Up: 7.7 Potential vorticity Matlab Previous: 7.7.4 Technical details   Contents
mitgcm-support@mitgcm.org
Copyright © 2006 Massachusetts Institute of Technology Last update 2018-01-23